3.9 Family 5 of analysis : multivariate analysis

Multivariate analysis can answer to multiple objective. One of them can be to study diversity structure and identify parents to cross based on either good complementarity or similarity for some traits

3.9.1 Decision tree

To study diversity structure and identify parents to cross based on either good complementarity or similarity for some traits, different scenario are possible (Figure 3.29). It can be completed by analysis of molecular data and genetic distance trees (M3, section 5).

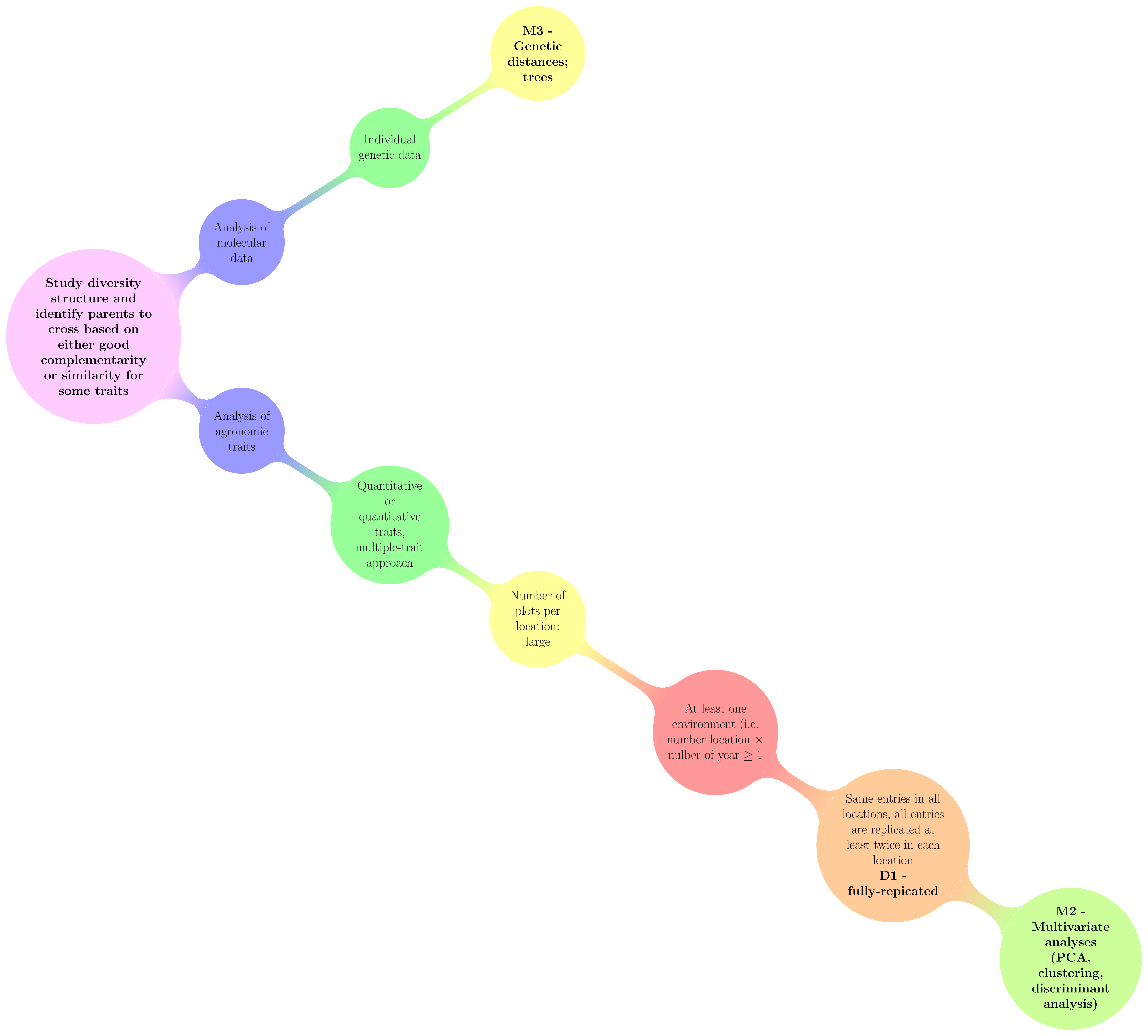
Decision tree with experimental constraints, designs and methods of agronomic analysis carry out in `PPBstats` regarding the objective :Study diversity structure and identify parents to cross based on either good complementarity or similarity for some traits. **D** refers to designs and **M** to methods.

Figure 3.29: Decision tree with experimental constraints, designs and methods of agronomic analysis carry out in PPBstats regarding the objective :Study diversity structure and identify parents to cross based on either good complementarity or similarity for some traits. D refers to designs and M to methods.

3.9.2 Workflow and function relations in `PPBstats` regarding family 2 of analysis

Figure 3.30 displays the functions and their relationships. Table 3.6 describes each of the main functions.

You can have more information for each function by typing ?function_name in your R session.

Figure 3.30: Main functions used in the workflow of family 5.

Table 3.6: Function description.
function name	description
`design_experiment`	Provides experimental design for the different situations corresponding to the choosen family of analysis
`format_data_PPBstats`	Check and format the data to be used in `PPBstats` functions
`ggcorrplot`	Visualize correlation with `ggcorrplot` fonction from package `ggcorrplot`
`multivariate`	Run multivariate analysis with functions from `FactoMineR`
`factoextra`	Check outputs and results with the `factoextra` package

3.9.3 Steps with `PPBstats`

For variance intra analysis, you can follow these steps (Figure 3.2) :

Format the data with format_data_PPBstats()
Look at correlation between variables with ggcorrplot::ggcorrplot()¹²
Run the analysis with multivariate()
Check outputs and results with functions from factoextra¹³

3.9.4 Format the data

data("data_model_GxE")
data_model_GxE = format_data_PPBstats(data_model_GxE, type = "data_agro")

## data has been formated for PPBstats functions.

3.9.5 Look at correlation

library(ggcorrplot)
vec_variables = c("y1", "y2", "y3")
corr = round(cor(data_model_GxE[,vec_variables]), 1)
p.mat = cor_pmat(data_model_GxE[,vec_variables])

# Barring the no significant coefficient
ggcorrplot(corr, hc.order = TRUE, type = "lower", p.mat = p.mat)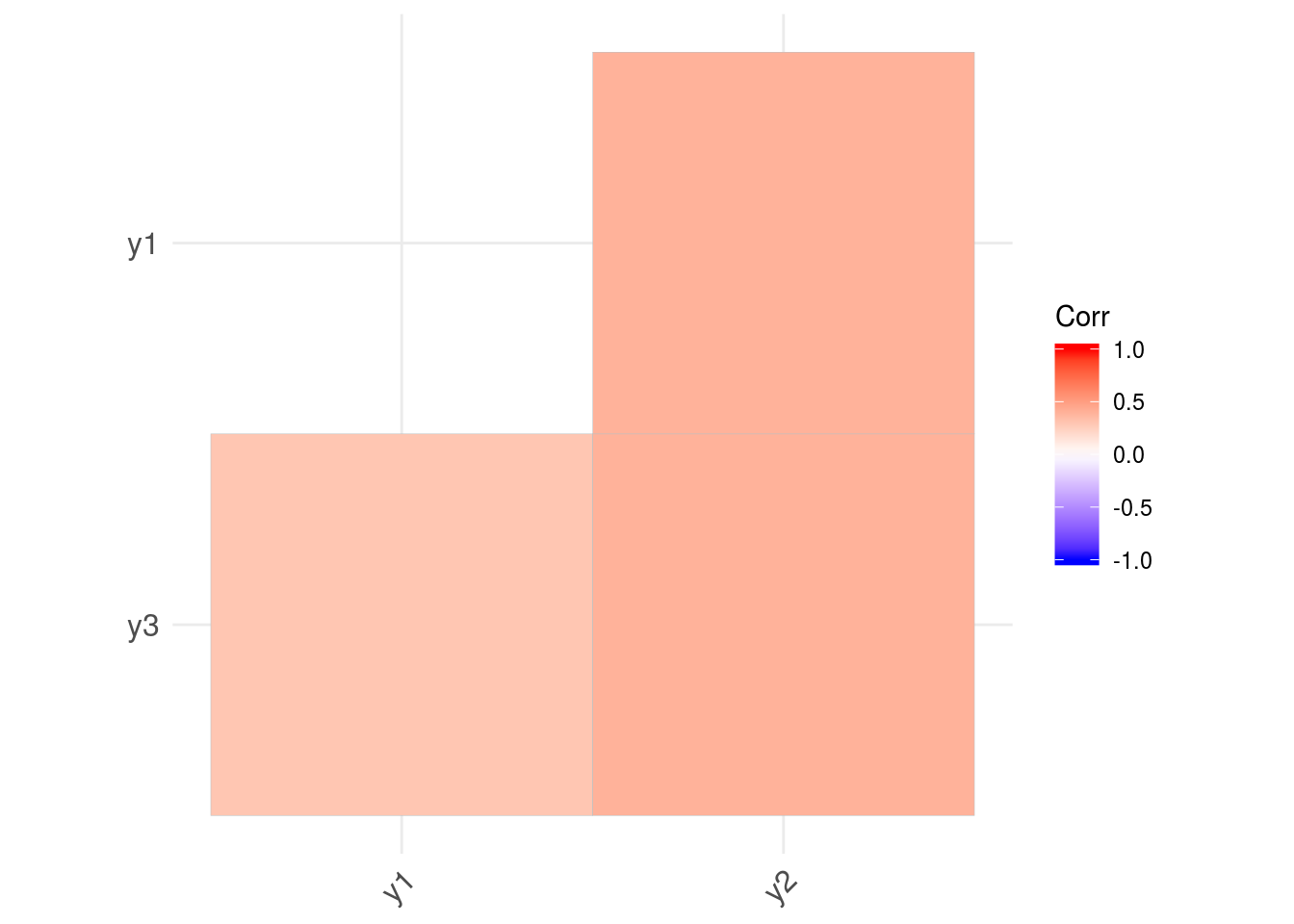

More details on the use of ggcorrplot() can be found here.

3.9.6 Run the analysis

vec_variables = c("y1", "y2", "y3")
res.pca = mutlivariate(data_model_GxE, vec_variables, PCA)

3.9.7 Check outputs and results

Look at the results thanks to the factoextra package:

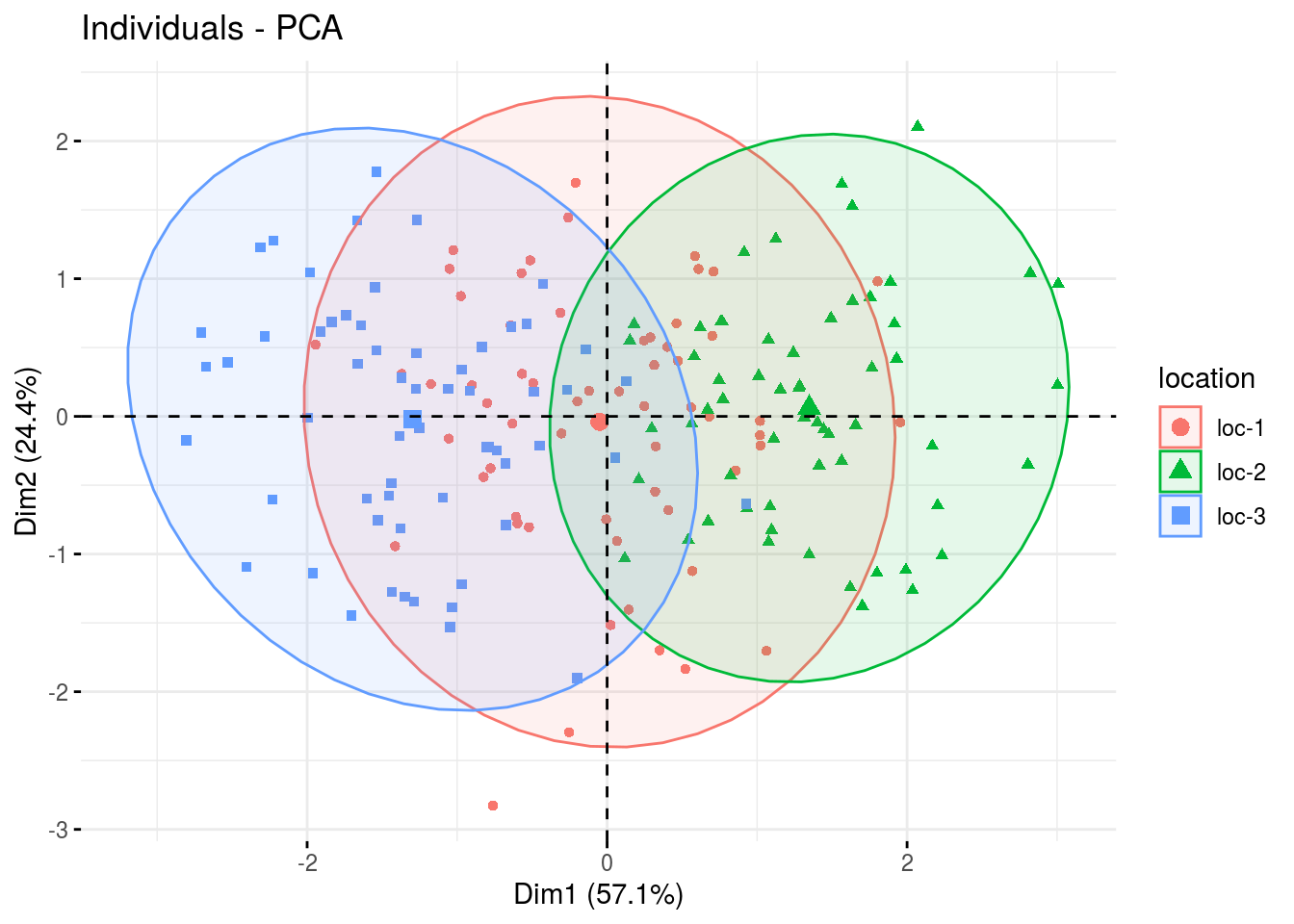
fviz_eig(res.pca)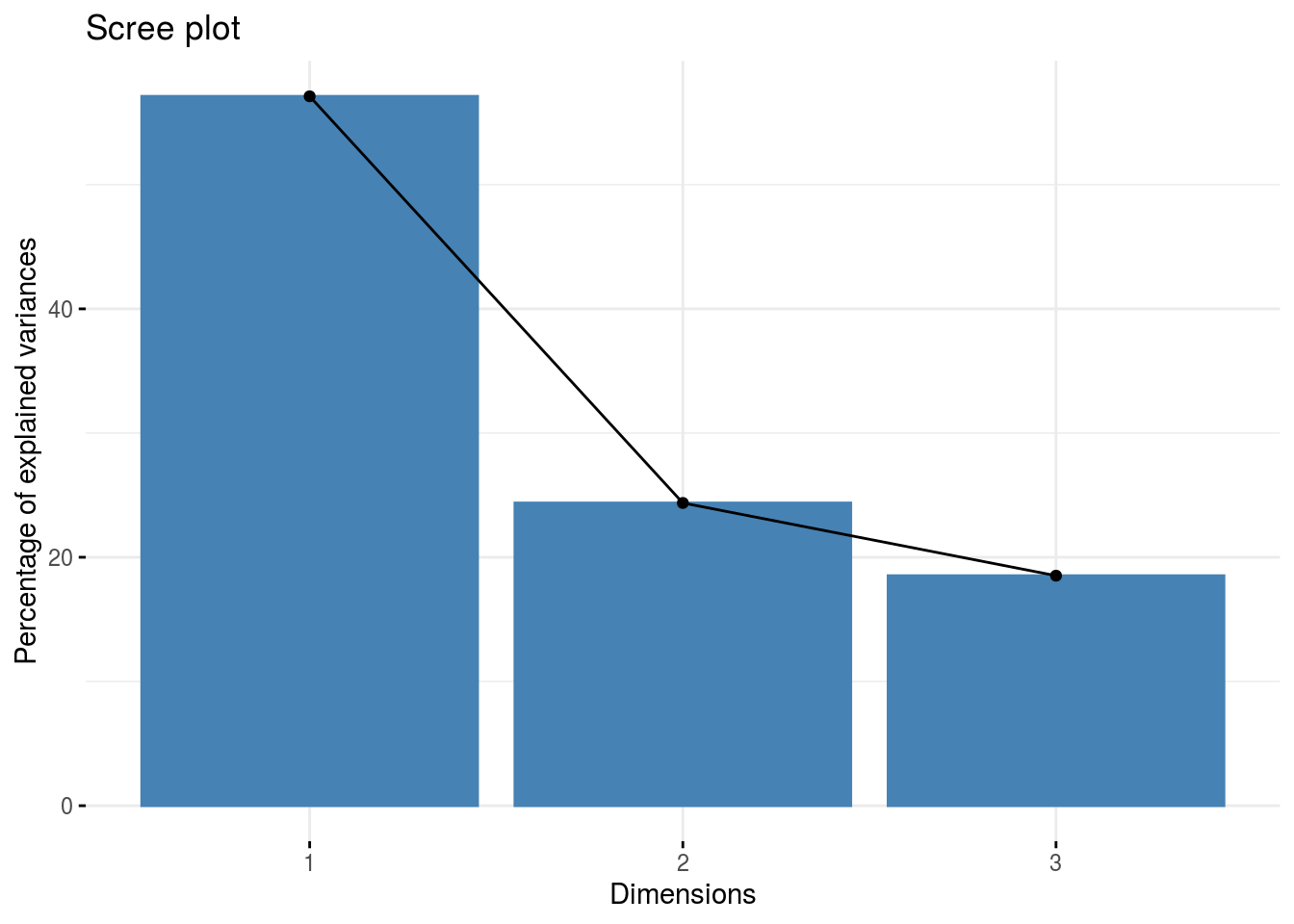

fviz_pca_ind(res.pca, label="none", habillage="location", addEllipses=TRUE, ellipse.level=0.95)