3.5 Family 1 of analysis : Compare different varieties evaluated for selection in different locations.

Family 1 gathers analyses that estimate entry effects. It allows to compare different entries on each location and test for significant differences among entries. Specific analysis including response to selection can also be done. The objective to compare different germplasms on each location for selection.

3.5.1 Decision tree

To compare different germplasms on each location for selection, different scenarios are possible (Figure 3.22) :

classic anova (M4a, section 3.5.3) based on on fully replicated designs (D1, section 3.2.1),
spatial analysis (M4b, section 3.5.4) based on row-column designs (D3, section 3.2.3),
mixed models (M5, section3.5.5) for incomplete blocks designs (D2, section 3.2.2),
bayesian hierarchical model intra-location (M7a, section 3.5.6) based on satellite-regional farms designs (D4, section 3.2.4).

It can be completed by organoleptic analysis (section 4). Based on these analysis, specific objective including response to selection analysis can also be done.

Decision tree with experimental constraints, designs and methods of agronomic analysis carry out in `PPBstats` regarding the objective : Compare different varieties evaluated for selection in different locations. **D** refers to designs and **M** to methods.

Figure 3.22: Decision tree with experimental constraints, designs and methods of agronomic analysis carry out in PPBstats regarding the objective : Compare different varieties evaluated for selection in different locations. D refers to designs and M to methods.

3.5.2 Workflow and function relations in `PPBstats` regarding family 1 of analysis

Figure 3.23 displays the functions and their relationships. Table 3.2 describes each of the main functions.

You can have more information for each function by typing ?function_name in your R session. Note that check_model(), mean_comparison() and plot() are S3 method. Therefore, you should type ?check_model, ?mean_comparison or ?plot.PPBstats to have general features and then see in details for specific functions.

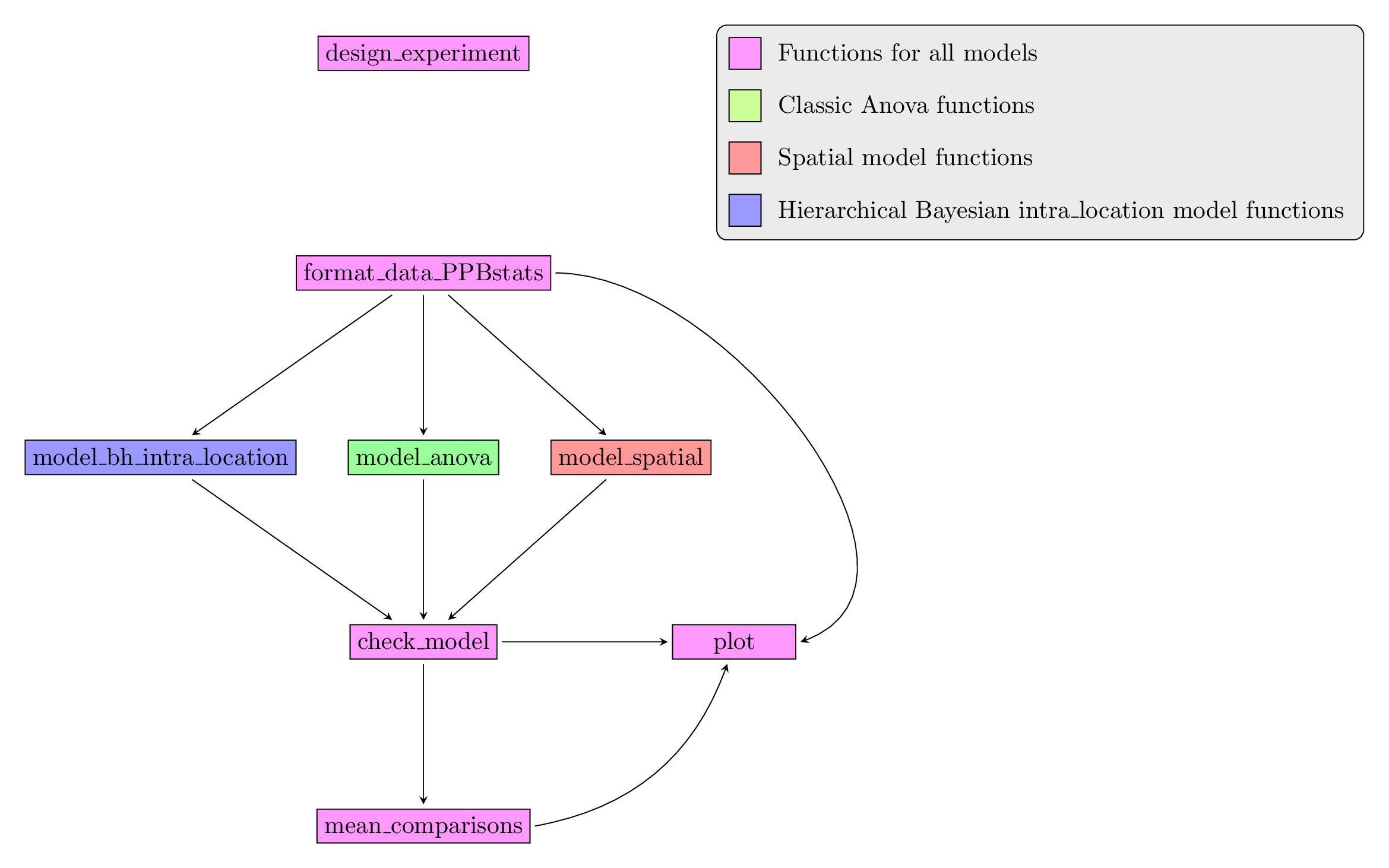
Figure 3.23: Main functions used in the workflow of family 1.

Table 3.2: Function description.
function name	description
`design_experiment`	Provides experimental design for the different situations corresponding to the choosen family of analysis
`format_data_PPBstats`	Check and format the data to be used in `PPBstats` functions
`model_bh_intra-location`	Run Hierarchical Bayesian intra-location model
`model_spatial`	Run spatial row and column model
`model_anova`	Run classic anova model
`check_model`	Check if the model went well
`mean_comparisons`	Get mean comparisons
`plot`	Build ggplot objects to visualize output

3.5.3 Classic ANOVA (M4a)

3.5.3.1 Theory of the model

The experimental design used is fully replicated (D1) on one location. The model is based on frequentist statistics (section 3.1.2.1). The tests to check the model are explained in section 3.1.2.1.2. The method to compute mean comparison are explained in section 3.1.2.1.3. The analysis is done the following model :

\(Y_{ijk} = \mu + \alpha_{i} + rep_{k} + \varepsilon_{ijk}; \quad \varepsilon_{ijk} \sim \mathcal{N} (0,\sigma^2)\)

With,

\(Y_{ijk}\) the phenotypic value for replication \(k\), germplasm \(i\) and individual \(j\),
\(\mu\) the general mean,
\(\alpha_{i}\) the effect of germplasm \(i\),
\(rep_{k}\) the effect of the replication \(k\),
\(\varepsilon_{ijk}\) the residuals.

3.5.3.2 Steps with `PPBstats`

For classic anova analysis, you can follow these steps (Figure 3.2):

Format the data with format_data_PPBstats()
Run the model with model_anova
Check model outputs to know if you can continue the analysis with check_model() and vizualise it with plot()
Get mean comparisons for each factor with mean_comparisons() and vizualise it with plot()

3.5.3.3 Format the data

A subset of data_model_GxE is used in this exemple.

data(data_model_GxE)
data_model_anova = droplevels(dplyr::filter(data_model_GxE, location == "loc-1"))  
data_model_anova = format_data_PPBstats(data_model_anova, type = "data_agro")

## data has been formated for PPBstats functions.

head(data_model_anova)

##                  seed_lot location     long      lat year germplasm block
## 1 germ-12_loc-1_2005_0001    loc-1 0.616363 44.20314 2005   germ-12     1
## 2  germ-1_loc-1_2005_0001    loc-1 0.616363 44.20314 2005    germ-1     1
## 3 germ-18_loc-1_2005_0001    loc-1 0.616363 44.20314 2005   germ-18     1
## 4 germ-14_loc-1_2005_0001    loc-1 0.616363 44.20314 2005   germ-14     1
## 5  germ-6_loc-1_2005_0001    loc-1 0.616363 44.20314 2005    germ-6     1
## 6  germ-4_loc-1_2005_0001    loc-1 0.616363 44.20314 2005    germ-4     1
##   X Y       y1    y1$date       y2    y2$date       y3    y3$date desease
## 1 A 1 14.32724 2017-07-15 41.85377 2017-07-15 66.05498 2017-07-15     low
## 2 A 2 23.03428 2017-07-15 37.38970 2017-07-15 63.39528 2017-07-15     low
## 3 A 3 24.91349 2017-07-15 38.38628 2017-07-15 60.52710 2017-07-15    high
## 4 A 4 24.99078 2017-07-15 39.72205 2017-07-15 60.80393 2017-07-15     low
## 5 A 5 18.95340 2017-07-15 46.60443 2017-07-15 53.71210 2017-07-15    high
## 6 B 1 21.31660 2017-07-15 49.94656 2017-07-15 60.71978 2017-07-15  medium
##   vigor y1$date_julian y2$date_julian y3$date_julian
## 1     l            195            195            195
## 2     l            195            195            195
## 3     h            195            195            195
## 4     l            195            195            195
## 5     m            195            195            195
## 6     l            195            195            195

3.5.3.4 Run the model

To run model on the dataset, used the function model_anova. You can run it on one variable.

out_anova = model_anova(data_model_anova, variable = "y1")

out_anova is a list containing two elements :

info : a list with variable

out_anova$info

## $variable
## [1] "y1"

ANOVA a list with two elements :

model

out_anova$ANOVA$model

## 
## Call:
## stats::lm(formula = variable ~ germplasm + block, data = data)
## 
## Coefficients:
## (Intercept)   germplasm1   germplasm2   germplasm3   germplasm4  
##    20.26702      1.60183      0.02397     -0.39822      1.21183  
##  germplasm5   germplasm6   germplasm7   germplasm8   germplasm9  
##     1.06590      3.76010     -5.10761     -0.92696      2.63546  
## germplasm10  germplasm11  germplasm12  germplasm13  germplasm14  
##     0.42415      1.56248     -5.76240     -4.62059      0.47600  
## germplasm15  germplasm16  germplasm17  germplasm18  germplasm19  
##     1.43492     -1.55346      0.89022      0.39441      1.16307  
##      block1       block2  
##    -0.93928     -0.22936

anova_model

out_anova$ANOVA$anova_model

## Analysis of Variance Table
## 
## Response: variable
##           Df  Sum Sq Mean Sq F value Pr(>F)
## germplasm 19  361.54  19.028  0.5090 0.9414
## block      2   46.01  23.006  0.6154 0.5457
## Residuals 38 1420.67  37.386

germplasm_effects a list of two elements :

effects

out_anova$ANOVA$germplasm_effects$effects

##      germ-1     germ-10     germ-11     germ-12     germ-13     germ-14 
##  1.60183489  0.02396579 -0.39821799  1.21183407  1.06590372  3.76009917 
##     germ-15     germ-16     germ-17     germ-18     germ-19      germ-2 
## -5.10761419 -0.92695642  2.63546203  0.42415203  1.56247594 -5.76239571 
##     germ-20      germ-3      germ-4      germ-5      germ-6      germ-7 
## -4.62059183  0.47600360  1.43491926 -1.55346262  0.89022028  0.39441135 
##      germ-8      germ-9 
##  1.16306897  1.72488766

intra_variance

out_anova$ANOVA$germplasm_effects$intra_variance

##     germ-1    germ-10    germ-11    germ-12    germ-13    germ-14 
##  14.550965 204.517046  28.558887  45.376513  51.105885   3.216895 
##    germ-15    germ-16    germ-17    germ-18    germ-19     germ-2 
##  21.434155  19.650429  28.827606  24.862755  80.733922   2.938909 
##    germ-20     germ-3     germ-4     germ-5     germ-6     germ-7 
##  17.722408  43.102002  10.437349  37.931023  13.113586  44.667769 
##     germ-8     germ-9 
##   7.226053  10.361250

3.5.3.5 Check and visualize model outputs

The tests to check the model are explained in section 3.1.2.1.2.

3.5.3.5.1 Check the model

Once the model is run, it is necessary to check if the outputs can be taken with confidence. This step is needed before going ahead in the analysis (in fact, object used in the next functions must come from check_model()).

out_check_anova = check_model(out_anova)

out_check_anova is a list containing four elements :

info : a list with variable
model_anova the output from the model
data_ggplot a list containing information for ggplot:
- data_ggplot_residuals a list containing :
  - data_ggplot_normality
  - data_ggplot_skewness_test
  - data_ggplot_kurtosis_test
  - data_ggplot_qqplot
- data_ggplot_variability_repartition_pie
- data_ggplot_var_intra

3.5.3.5.2 Visualize outputs

Once the computation is done, you can visualize the results with plot()

p_out_check_anova = plot(out_check_anova)

p_out_check_anova is a list with:

residuals

histogram : histogram with the distribution of the residuals

p_out_check_anova$residuals$histogram

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.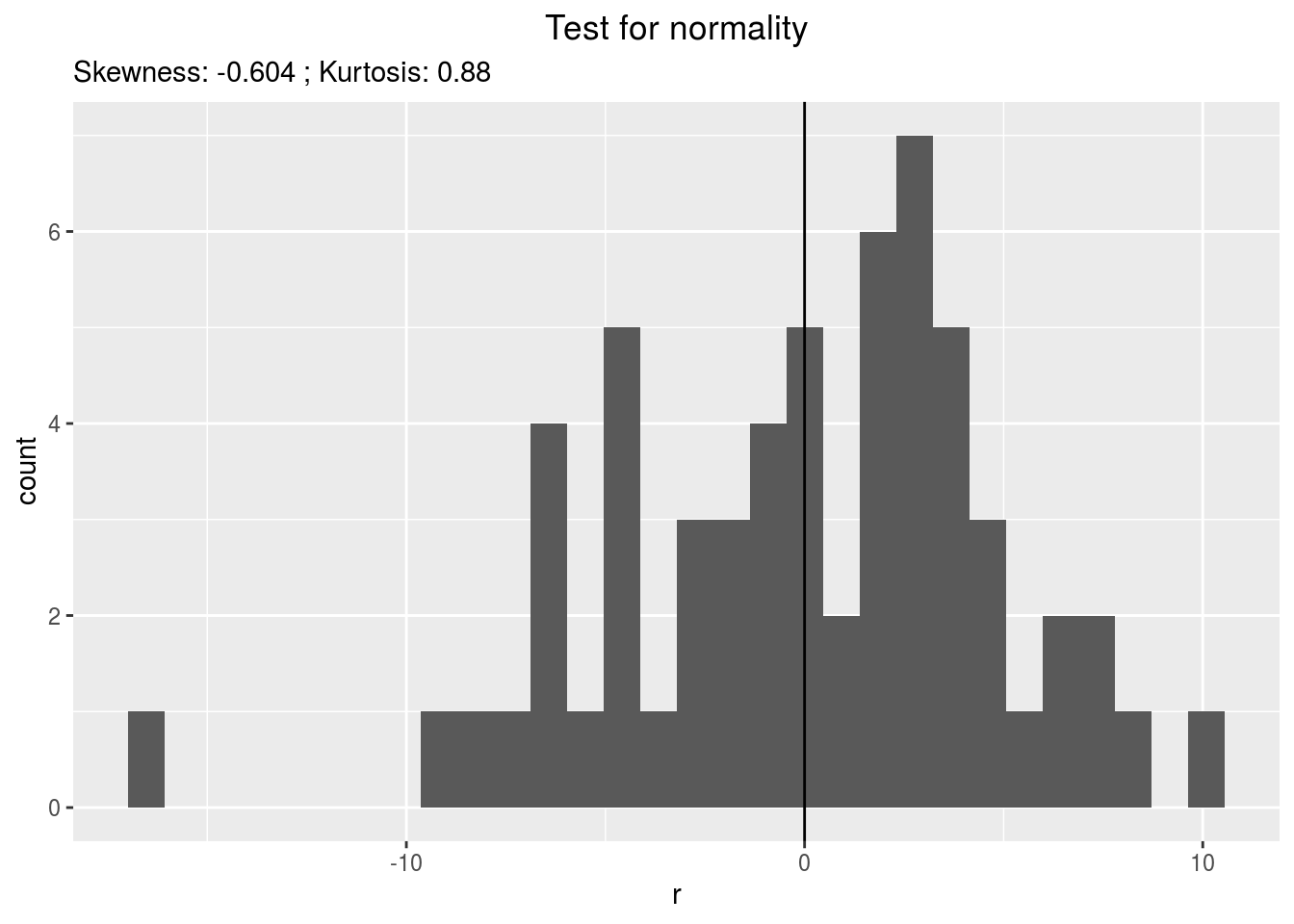

qqplot

p_out_check_anova$residuals$qqplot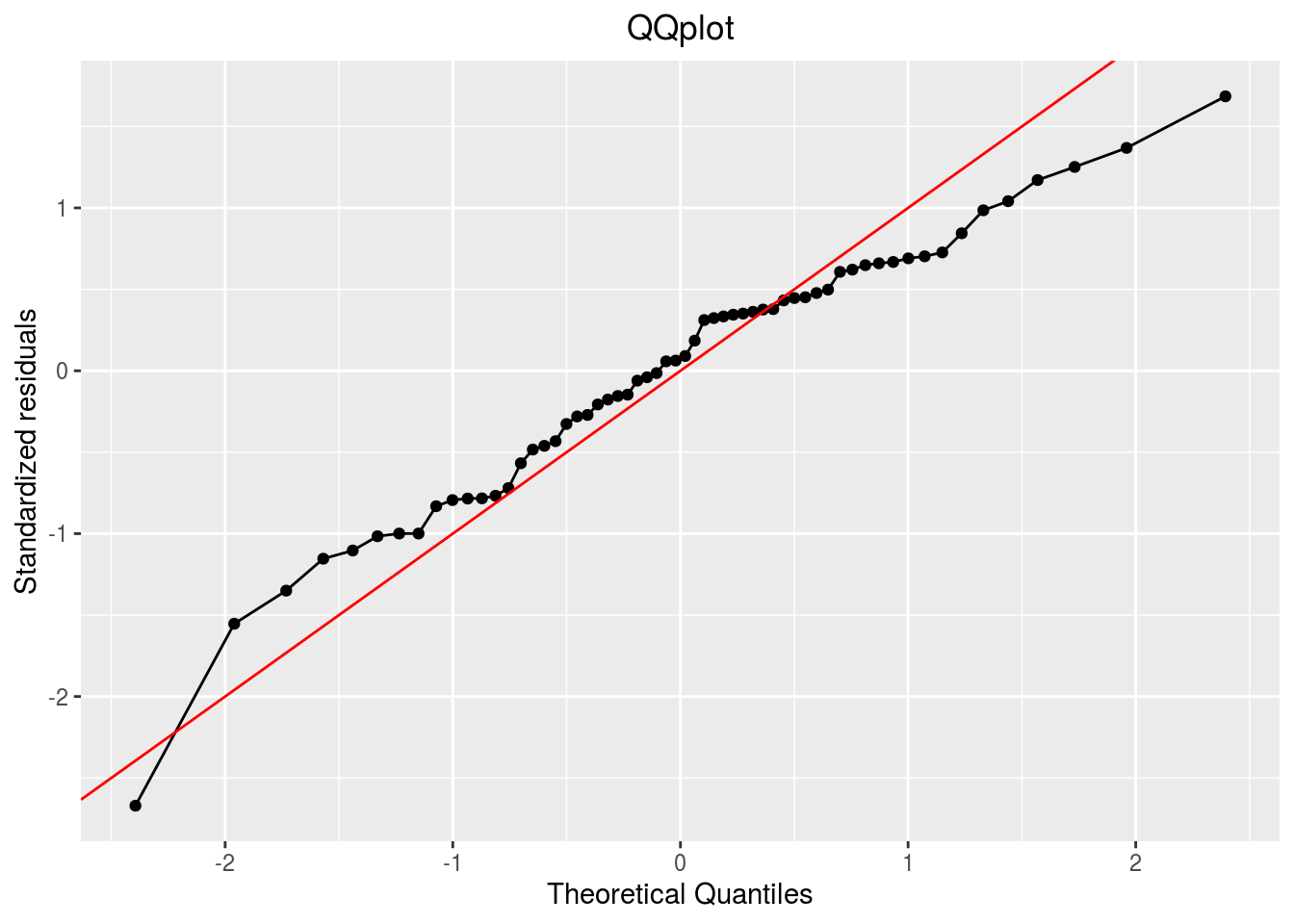

variability_repartition : pie with repartition of SumSq for each factor

p_out_check_anova$variability_repartition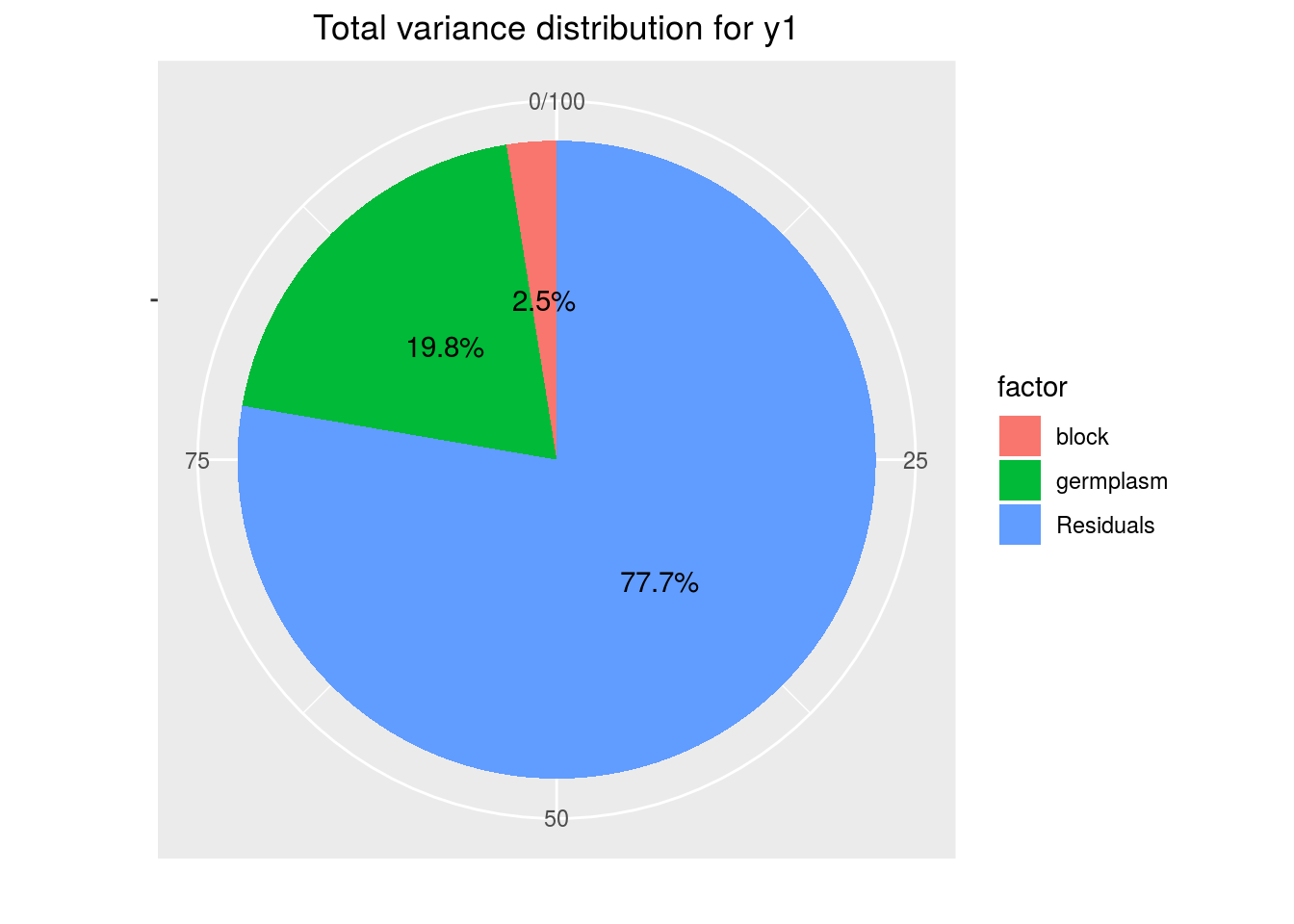

variance_intra_germplasm : repartition of the residuals for each germplasm (see Details for more information) With the hypothesis than the micro-environmental variation is equaly distributed on all the individuals (i.e. all the plants), the distribution of each germplasm represent the intra-germplasm variance. This has to been seen with caution:
- If germplasm have no intra-germplasm variance (i.e. pure line or hybrides) then the distribution of each germplasm represent only the micro-environmental variation.
- If germplasm have intra-germplasm variance (i.e. population such as landraces for example) then the distribution of each germplasm represent the micro-environmental variation plus the intra-germplasm variance.

p_out_check_anova$variance_intra_germplasm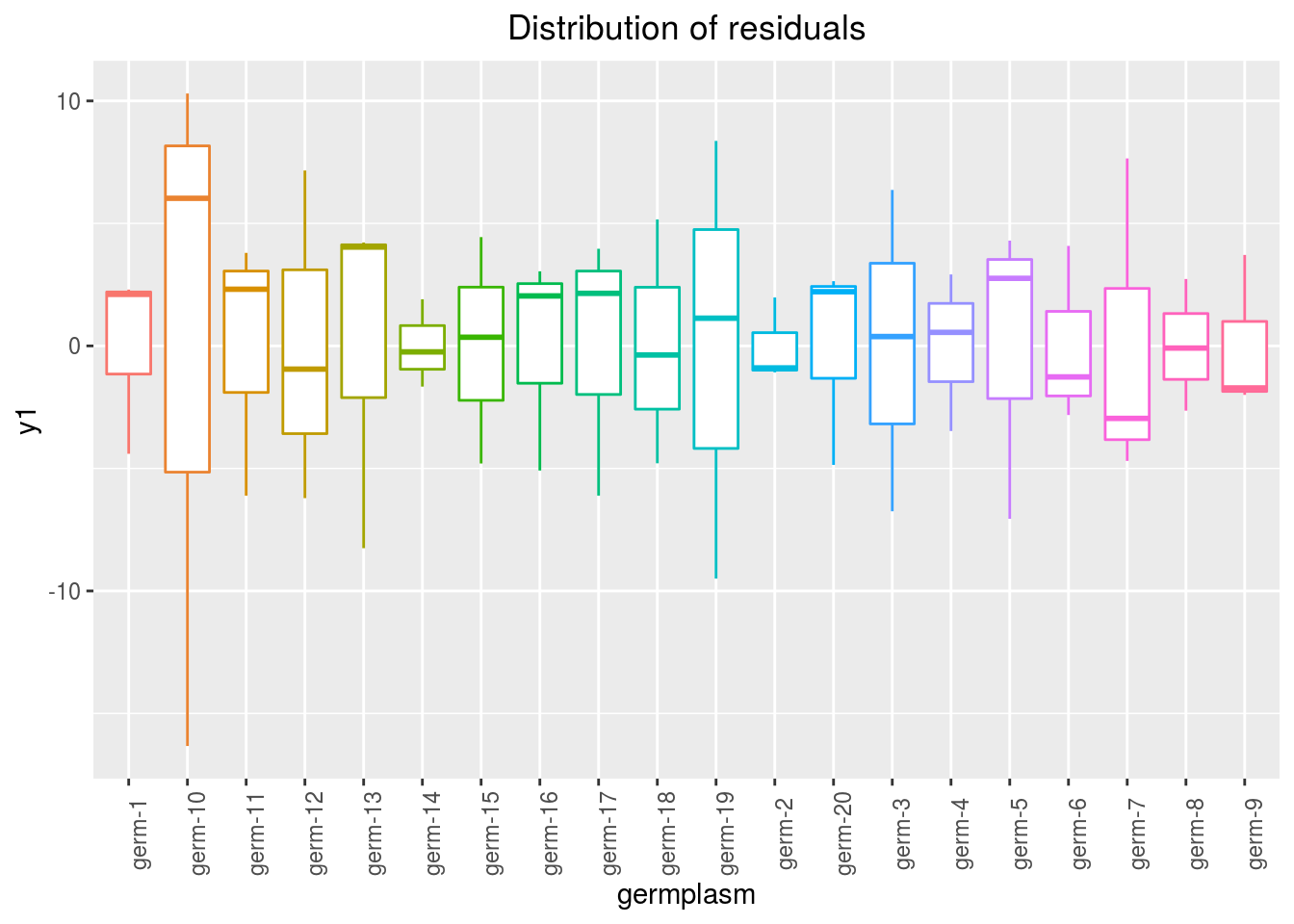

3.5.3.6 Get and visualize mean comparisons

The method to compute mean comparison are explained in section 3.1.2.1.3.

3.5.3.6.1 Get mean comparisons

Get mean comparisons with mean_comparisons().

out_mean_comparisons_anova = mean_comparisons(out_check_anova, p.adj = "bonferroni")

out_mean_comparisons_anova is a list of two elements:

info : a list with variable
data_ggplot_LSDbarplot_germplasm

3.5.3.6.2 Visualize mean comparisons

p_out_mean_comparisons_anova = plot(out_mean_comparisons_anova)

p_out_mean_comparisons_anova is a list of one element with barplots :

For each element of the list, there are as many graph as needed with nb_parameters_per_plot parameters per graph. Letters are displayed on each bar. Parameters that do not share the same letters are different regarding type I error (alpha) and alpha correction. The error I (alpha) and the alpha correction are displayed in the title.

germplasm : mean comparison for germplasm

pg = p_out_mean_comparisons_anova$germplasm
names(pg)

## [1] "1" "2" "3"

pg$`1`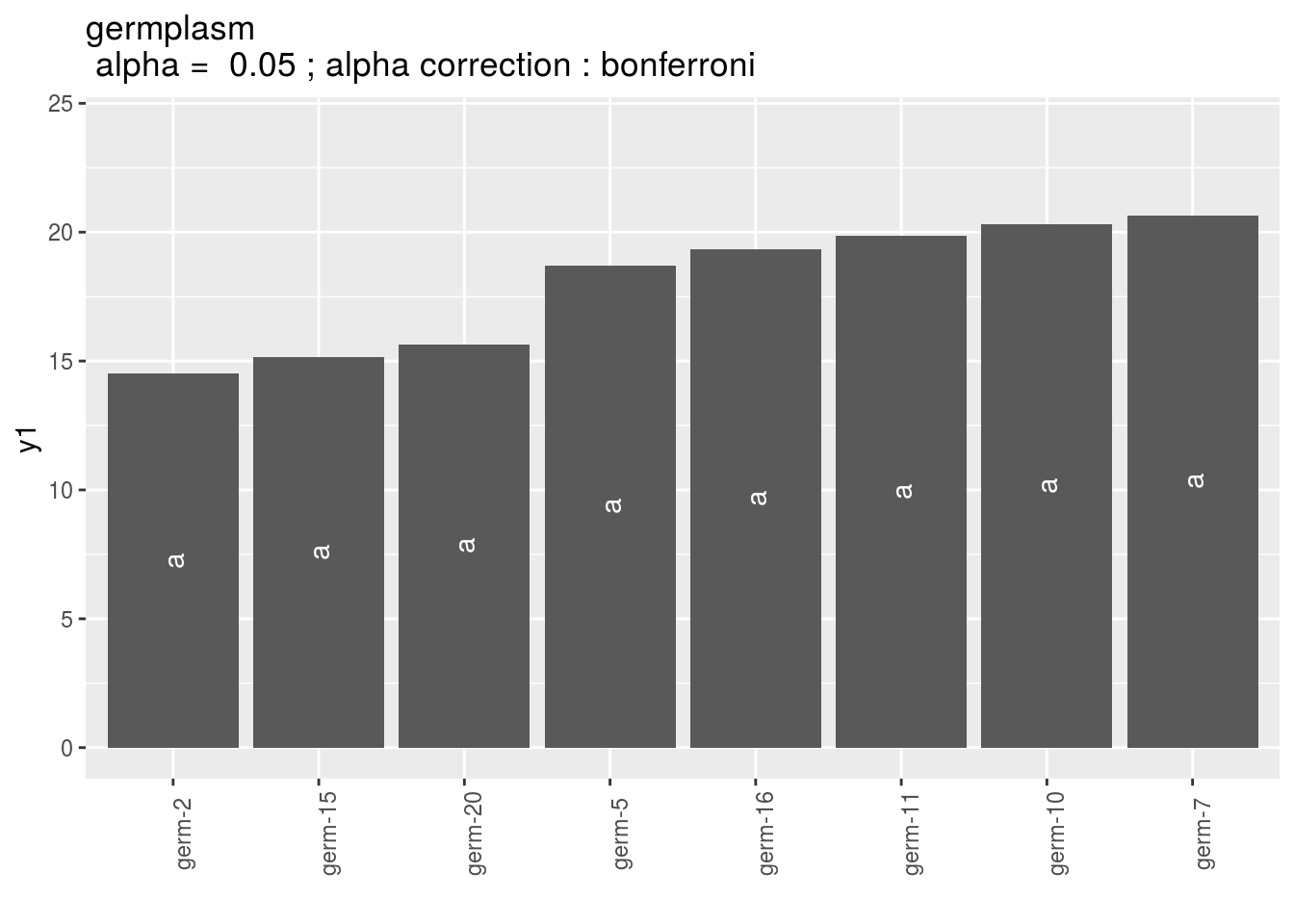

3.5.4 Spatial analysis (M4b)

3.5.4.1 Theory of the model

The experimental design used is the row-column design (D3). The following model is based on frequentist statistics (section 3.1.2.1). The model allows taking into account environmental variation within a block with few control replicated in rows and columns.

It is based on a SpATS (Spatial Analysis of Field Trials with Splines) model proposed by Rodrı'guez-Álvarez et al. (2016) :

\(Y_{ijk} = \alpha_{i} + r_{j} + c_{k} + f(u,v) + \varepsilon_{ijk}; \quad \varepsilon_{ijk} \sim \mathcal{N} (0,\sigma^2)\)

With,

\(Y_{ijk}\) the phenotypic value for germplasm \(i\), row \(j\) and column \(k\)
\(\alpha_{i}\) the random effect of germplasm \(i\)
\(r_{j}\) the effect of row \(j\)
\(c_{k}\) the effect of col \(k\)
\(f(u,v)\) the smooth bivariate function that simultaneously accounts for the spatial trend across both directions of the fiel (i.e. rows and columns)
\(\varepsilon_{ijk}\) the residuals

Note that \(f(u,v)\) is divided into 8 components excluding the intercept (Rodrı'guez-Álvarez et al. 2016):

the linear effect of the rows (row),
the linear effect of the columns (col),
the linear interaction of rows and columns (row:col),
the main row effect (f(row)),
the main column effect (f(col)),
the smooth varying coefficient term regarding rows (f(col):row),
the smooth varying coefficient term regarding columns (row:f(col))),
the smooth-by-smooth interaction component (f(col):f(row))

Much more information regarding the model as well as example of R package SpATS can be found in Rodrı'guez-Álvarez et al. (2016).

3.5.4.2 Steps with `PPBstats`

Format the data with format_data_PPBstats()
Run the model with model_spatial()
Check model outputs with graphs to know if you can continue the analysis with check_model() and vizualise it with plot()
Get mean comparisons for germplasms with mean_comparisons() and vizualise it with plot()

3.5.4.3 Format the data

data("data_model_spatial")
data_model_spatial = format_data_PPBstats(data_model_spatial, type = "data_agro")

## Warning in format_data_PPBstats.data_agro(data): Column "long" is needed to
## get map and not present in data.

## Warning in format_data_PPBstats.data_agro(data): Column "lat" is needed to
## get map and not present in data.

## data has been formated for PPBstats functions.

3.5.4.4 Run the model

By default, germplasm are settled as random.

out_spatial = model_spatial(data = data_model_spatial, variable = "y1")

## Effective dimensions
## -------------------------
## It.     Deviance   germplasm       col_f       row_f      f(col)      f(row)  f(col):row  col:f(row)f(col):f(row)
##   1 32230.908352      77.713       0.721       0.358      11.835       0.260      10.118       0.259       5.122
##   2  1381.145352      78.477       0.842       0.688       8.927       0.162       7.951       0.300       5.322
##   3  1372.535535      79.099       0.960       0.978       6.672       0.076       6.337       0.322       5.415
##   4  1366.744421      79.500       1.074       1.125       4.901       0.028       5.204       0.322       5.489
##   5  1363.081900      79.535       1.181       1.172       3.519       0.009       4.528       0.301       5.636
##   6  1360.738664      79.195       1.281       1.182       2.449       0.003       4.155       0.269       5.922
##   7  1359.521819      78.552       1.374       1.182       1.701       0.001       3.934       0.235       6.325
##   8  1359.207730      77.656       1.457       1.181       1.397       0.000       3.769       0.206       6.764
##   9  1359.079764      76.642       1.536       1.180       1.327       0.000       3.621       0.183       7.188
##  10  1358.974057      75.611       1.617       1.178       1.304       0.000       3.485       0.164       7.578
##  11  1358.878185      74.585       1.701       1.175       1.290       0.000       3.356       0.147       7.934
##  12  1358.787396      73.571       1.787       1.171       1.278       0.000       3.228       0.132       8.256
##  13  1358.697592      72.570       1.875       1.168       1.268       0.000       3.098       0.119       8.547
##  14  1358.604502      71.580       1.965       1.165       1.258       0.000       2.960       0.107       8.810
##  15  1358.503034      70.600       2.057       1.161       1.249       0.000       2.813       0.096       9.051
##  16  1358.386490      69.626       2.151       1.158       1.240       0.000       2.649       0.087       9.272
##  17  1358.245521      68.654       2.246       1.155       1.231       0.000       2.464       0.078       9.478
##  18  1358.066927      67.679       2.343       1.151       1.223       0.000       2.252       0.070       9.672
##  19  1357.832952      66.698       2.440       1.147       1.215       0.000       2.004       0.063       9.859
##  20  1357.522974      65.703       2.536       1.143       1.208       0.000       1.715       0.056      10.042
##  21  1357.121302      64.692       2.632       1.139       1.202       0.000       1.379       0.050      10.220
##  22  1356.636368      63.663       2.725       1.136       1.198       0.000       0.999       0.044      10.392
##  23  1356.137281      62.621       2.817       1.134       1.195       0.000       0.592       0.039      10.551
##  24  1355.764187      61.561       2.910       1.133       1.192       0.000       0.249       0.035      10.684
##  25  1355.579891      60.477       3.005       1.133       1.188       0.000       0.074       0.031      10.776
##  26  1355.502334      59.399       3.103       1.134       1.185       0.000       0.018       0.028      10.840
##  27  1355.460151      58.356       3.203       1.134       1.182       0.000       0.004       0.025      10.889
##  28  1355.428453      57.354       3.304       1.134       1.179       0.000       0.001       0.022      10.929
##  29  1355.400641      56.393       3.406       1.134       1.177       0.000       0.000       0.020      10.962
##  30  1355.374996      55.469       3.509       1.134       1.175       0.000       0.000       0.018      10.990
##  31  1355.350988      54.579       3.613       1.134       1.174       0.000       0.000       0.016      11.013
##  32  1355.328384      53.722       3.716       1.134       1.172       0.000       0.000       0.015      11.032
##  33  1355.307038      52.894       3.820       1.134       1.170       0.000       0.000       0.013      11.047
##  34  1355.286835      52.094       3.924       1.134       1.169       0.000       0.000       0.012      11.059
##  35  1355.267678      51.319       4.027       1.134       1.168       0.000       0.000       0.011      11.069
##  36  1355.249485      50.569       4.129       1.133       1.166       0.000       0.000       0.010      11.077
##  37  1355.232183      49.841       4.231       1.133       1.165       0.000       0.000       0.009      11.083
##  38  1355.215708      49.134       4.331       1.133       1.164       0.000       0.000       0.008      11.087
##  39  1355.200003      48.448       4.431       1.133       1.162       0.000       0.000       0.008      11.090
##  40  1355.185015      47.779       4.529       1.133       1.161       0.000       0.000       0.007      11.092
##  41  1355.170700      47.129       4.625       1.133       1.160       0.000       0.000       0.006      11.093
##  42  1355.157014      46.495       4.719       1.133       1.159       0.000       0.000       0.006      11.093
##  43  1355.143919      45.877       4.812       1.133       1.158       0.000       0.000       0.005      11.093
##  44  1355.131378      45.275       4.902       1.133       1.157       0.000       0.000       0.005      11.092
##  45  1355.119359      44.686       4.990       1.133       1.156       0.000       0.000       0.005      11.090
##  46  1355.107831      44.111       5.077       1.133       1.155       0.000       0.000       0.004      11.088
##  47  1355.096764      43.549       5.160       1.133       1.154       0.000       0.000       0.004      11.086
##  48  1355.086132      43.000       5.242       1.133       1.153       0.000       0.000       0.004      11.084
##  49  1355.075909      42.462       5.320       1.133       1.152       0.000       0.000       0.003      11.081
##  50  1355.066070      41.936       5.397       1.133       1.151       0.000       0.000       0.003      11.078
##  51  1355.056594      41.420       5.471       1.133       1.151       0.000       0.000       0.003      11.075
##  52  1355.047459      40.915       5.542       1.133       1.150       0.000       0.000       0.003      11.072
##  53  1355.038645      40.419       5.611       1.133       1.149       0.000       0.000       0.003      11.069
##  54  1355.030133      39.933       5.677       1.133       1.148       0.000       0.000       0.002      11.066
##  55  1355.021905      39.457       5.741       1.133       1.148       0.000       0.000       0.002      11.063
##  56  1355.013944      38.989       5.803       1.133       1.147       0.000       0.000       0.002      11.060
##  57  1355.006234      38.529       5.862       1.132       1.146       0.000       0.000       0.002      11.057
##  58  1354.998761      38.078       5.919       1.132       1.146       0.000       0.000       0.002      11.054
##  59  1354.991511      37.634       5.974       1.132       1.145       0.000       0.000       0.002      11.051
##  60  1354.984470      37.198       6.026       1.132       1.145       0.000       0.000       0.002      11.048
##  61  1354.977626      36.769       6.076       1.132       1.144       0.000       0.000       0.001      11.045
##  62  1354.970968      36.347       6.124       1.132       1.143       0.000       0.000       0.001      11.042
##  63  1354.964484      35.931       6.170       1.132       1.143       0.000       0.000       0.001      11.040
##  64  1354.958165      35.522       6.215       1.132       1.143       0.000       0.000       0.001      11.037
##  65  1354.952001      35.120       6.257       1.132       1.142       0.000       0.000       0.001      11.034
##  66  1354.945982      34.723       6.297       1.132       1.142       0.000       0.000       0.001      11.032
##  67  1354.940102      34.332       6.336       1.132       1.141       0.000       0.000       0.001      11.029
##  68  1354.934351      33.946       6.373       1.132       1.141       0.000       0.000       0.001      11.027
##  69  1354.928723      33.566       6.409       1.132       1.140       0.000       0.000       0.001      11.024
##  70  1354.923210      33.192       6.443       1.132       1.140       0.000       0.000       0.001      11.022
##  71  1354.917807      32.822       6.476       1.132       1.140       0.000       0.000       0.001      11.020
##  72  1354.912506      32.457       6.507       1.132       1.139       0.000       0.000       0.001      11.018
##  73  1354.907303      32.096       6.537       1.132       1.139       0.000       0.000       0.001      11.015
##  74  1354.902193      31.740       6.566       1.132       1.139       0.000       0.000       0.001      11.013
##  75  1354.897169      31.389       6.593       1.132       1.138       0.000       0.000       0.001      11.011
##  76  1354.892228      31.042       6.619       1.132       1.138       0.000       0.000       0.001      11.009
##  77  1354.887365      30.698       6.645       1.132       1.138       0.000       0.000       0.001      11.008
##  78  1354.882575      30.359       6.669       1.132       1.138       0.000       0.000       0.001      11.006
##  79  1354.877856      30.024       6.692       1.132       1.137       0.000       0.000       0.000      11.004
##  80  1354.873202      29.692       6.715       1.132       1.137       0.000       0.000       0.000      11.002
##  81  1354.868612      29.364       6.736       1.131       1.137       0.000       0.000       0.000      11.000
##  82  1354.864081      29.039       6.757       1.131       1.137       0.000       0.000       0.000      10.999
##  83  1354.859606      28.718       6.777       1.131       1.137       0.000       0.000       0.000      10.997
##  84  1354.855184      28.400       6.796       1.131       1.136       0.000       0.000       0.000      10.995
##  85  1354.850813      28.085       6.814       1.131       1.136       0.000       0.000       0.000      10.994
##  86  1354.846490      27.774       6.832       1.131       1.136       0.000       0.000       0.000      10.992
##  87  1354.842212      27.465       6.849       1.131       1.136       0.000       0.000       0.000      10.991
##  88  1354.837977      27.159       6.866       1.131       1.136       0.000       0.000       0.000      10.989
##  89  1354.833783      26.856       6.882       1.131       1.135       0.000       0.000       0.000      10.988
##  90  1354.829627      26.556       6.897       1.131       1.135       0.000       0.000       0.000      10.986
##  91  1354.825508      26.258       6.912       1.131       1.135       0.000       0.000       0.000      10.985
##  92  1354.821423      25.963       6.927       1.131       1.135       0.000       0.000       0.000      10.984
##  93  1354.817371      25.671       6.941       1.131       1.135       0.000       0.000       0.000      10.982
##  94  1354.813349      25.381       6.954       1.131       1.135       0.000       0.000       0.000      10.981
##  95  1354.809357      25.093       6.967       1.131       1.135       0.000       0.000       0.000      10.979
##  96  1354.805391      24.808       6.980       1.131       1.135       0.000       0.000       0.000      10.978
##  97  1354.801452      24.525       6.992       1.131       1.134       0.000       0.000       0.000      10.977
##  98  1354.797537      24.244       7.004       1.131       1.134       0.000       0.000       0.000      10.975
##  99  1354.793645      23.965       7.016       1.131       1.134       0.000       0.000       0.000      10.974
## 100  1354.789774      23.689       7.027       1.131       1.134       0.000       0.000       0.000      10.973
## 101  1354.785923      23.414       7.038       1.131       1.134       0.000       0.000       0.000      10.971
## 102  1354.782091      23.142       7.049       1.131       1.134       0.000       0.000       0.000      10.970
## 103  1354.778277      22.871       7.059       1.131       1.134       0.000       0.000       0.000      10.969
## 104  1354.774480      22.603       7.070       1.130       1.134       0.000       0.000       0.000      10.968
## 105  1354.770697      22.336       7.080       1.130       1.134       0.000       0.000       0.000      10.966
## 106  1354.766929      22.071       7.089       1.130       1.134       0.000       0.000       0.000      10.965
## 107  1354.763175      21.808       7.099       1.130       1.134       0.000       0.000       0.000      10.964
## 108  1354.759432      21.546       7.108       1.130       1.133       0.000       0.000       0.000      10.962
## 109  1354.755701      21.287       7.117       1.130       1.133       0.000       0.000       0.000      10.961
## 110  1354.751980      21.029       7.125       1.130       1.133       0.000       0.000       0.000      10.960
## 111  1354.748268      20.773       7.134       1.130       1.133       0.000       0.000       0.000      10.958
## 112  1354.744566      20.518       7.142       1.130       1.133       0.000       0.000       0.000      10.957
## 113  1354.740871      20.265       7.150       1.130       1.133       0.000       0.000       0.000      10.956
## 114  1354.737183      20.014       7.158       1.130       1.133       0.000       0.000       0.000      10.954
## 115  1354.733501      19.764       7.166       1.130       1.133       0.000       0.000       0.000      10.953
## 116  1354.729825      19.516       7.174       1.130       1.133       0.000       0.000       0.000      10.952
## 117  1354.726154      19.269       7.181       1.130       1.133       0.000       0.000       0.000      10.950
## 118  1354.722487      19.024       7.189       1.130       1.133       0.000       0.000       0.000      10.949
## 119  1354.718824      18.780       7.196       1.130       1.133       0.000       0.000       0.000      10.948
## 120  1354.715164      18.538       7.203       1.130       1.133       0.000       0.000       0.000      10.946
## 121  1354.711506      18.297       7.209       1.130       1.133       0.000       0.000       0.000      10.945
## 122  1354.707850      18.058       7.216       1.130       1.133       0.000       0.000       0.000      10.943
## 123  1354.704196      17.820       7.223       1.130       1.133       0.000       0.000       0.000      10.942
## 124  1354.700543      17.584       7.229       1.130       1.133       0.000       0.000       0.000      10.940
## 125  1354.696890      17.349       7.235       1.130       1.133       0.000       0.000       0.000      10.939
## 126  1354.693238      17.115       7.242       1.130       1.133       0.000       0.000       0.000      10.937
## 127  1354.689585      16.883       7.248       1.129       1.133       0.000       0.000       0.000      10.936
## 128  1354.685931      16.652       7.253       1.129       1.133       0.000       0.000       0.000      10.934
## 129  1354.682277      16.422       7.259       1.129       1.133       0.000       0.000       0.000      10.933
## 130  1354.678622      16.194       7.265       1.129       1.133       0.000       0.000       0.000      10.931
## 131  1354.674964      15.967       7.270       1.129       1.133       0.000       0.000       0.000      10.930
## 132  1354.671305      15.742       7.276       1.129       1.133       0.000       0.000       0.000      10.928
## 133  1354.667645      15.518       7.281       1.129       1.133       0.000       0.000       0.000      10.927
## 134  1354.663982      15.295       7.286       1.129       1.133       0.000       0.000       0.000      10.925
## 135  1354.660316      15.074       7.291       1.129       1.133       0.000       0.000       0.000      10.923
## 136  1354.656648      14.854       7.296       1.129       1.133       0.000       0.000       0.000      10.922
## 137  1354.652978      14.636       7.301       1.129       1.133       0.000       0.000       0.000      10.920
## 138  1354.649304      14.418       7.306       1.129       1.133       0.000       0.000       0.000      10.919
## 139  1354.645629      14.203       7.310       1.129       1.133       0.000       0.000       0.000      10.917
## 140  1354.641950      13.988       7.315       1.129       1.133       0.000       0.000       0.000      10.915
## 141  1354.638268      13.775       7.319       1.129       1.133       0.000       0.000       0.000      10.913
## 142  1354.634584      13.564       7.324       1.129       1.133       0.000       0.000       0.000      10.912
## 143  1354.630898      13.353       7.328       1.129       1.133       0.000       0.000       0.000      10.910
## 144  1354.627208      13.145       7.332       1.129       1.133       0.000       0.000       0.000      10.908
## 145  1354.623517      12.937       7.336       1.129       1.133       0.000       0.000       0.000      10.906
## 146  1354.619823      12.731       7.340       1.129       1.133       0.000       0.000       0.000      10.904
## 147  1354.616127      12.527       7.344       1.129       1.133       0.000       0.000       0.000      10.903
## 148  1354.612429      12.324       7.347       1.129       1.133       0.000       0.000       0.000      10.901
## 149  1354.608730      12.122       7.351       1.129       1.133       0.000       0.000       0.000      10.899
## 150  1354.605029      11.922       7.354       1.129       1.133       0.000       0.000       0.000      10.897
## 151  1354.601327      11.724       7.358       1.128       1.133       0.000       0.000       0.000      10.895
## 152  1354.597625      11.527       7.361       1.128       1.133       0.000       0.000       0.000      10.893
## 153  1354.593922      11.331       7.364       1.128       1.133       0.000       0.000       0.000      10.891
## 154  1354.590220      11.137       7.367       1.128       1.133       0.000       0.000       0.000      10.889
## 155  1354.586518      10.945       7.371       1.128       1.134       0.000       0.000       0.000      10.887
## 156  1354.582817      10.754       7.373       1.128       1.134       0.000       0.000       0.000      10.885
## 157  1354.579118      10.564       7.376       1.128       1.134       0.000       0.000       0.000      10.883
## 158  1354.575420      10.377       7.379       1.128       1.134       0.000       0.000       0.000      10.881
## 159  1354.571725      10.191       7.382       1.128       1.134       0.000       0.000       0.000      10.879
## 160  1354.568034      10.006       7.384       1.128       1.134       0.000       0.000       0.000      10.877
## 161  1354.564346       9.823       7.387       1.128       1.134       0.000       0.000       0.000      10.875
## 162  1354.560662       9.642       7.389       1.128       1.134       0.000       0.000       0.000      10.872
## 163  1354.556984       9.463       7.392       1.128       1.134       0.000       0.000       0.000      10.870
## 164  1354.553311       9.285       7.394       1.128       1.134       0.000       0.000       0.000      10.868
## 165  1354.549644       9.109       7.396       1.128       1.134       0.000       0.000       0.000      10.866
## 166  1354.545985       8.934       7.398       1.128       1.134       0.000       0.000       0.000      10.864
## 167  1354.542334       8.762       7.400       1.128       1.134       0.000       0.000       0.000      10.862
## 168  1354.538692       8.591       7.402       1.128       1.135       0.000       0.000       0.000      10.859
## 169  1354.535059       8.422       7.404       1.128       1.135       0.000       0.000       0.000      10.857
## 170  1354.531436       8.255       7.405       1.128       1.135       0.000       0.000       0.000      10.855
## 171  1354.527825       8.090       7.407       1.128       1.135       0.000       0.000       0.000      10.852
## 172  1354.524226       7.926       7.408       1.128       1.135       0.000       0.000       0.000      10.850
## 173  1354.520639       7.764       7.410       1.128       1.135       0.000       0.000       0.000      10.848
## 174  1354.517067       7.604       7.411       1.128       1.135       0.000       0.000       0.000      10.845
## 175  1354.513509       7.446       7.413       1.127       1.135       0.000       0.000       0.000      10.843
## 176  1354.509967       7.290       7.414       1.127       1.135       0.000       0.000       0.000      10.841
## 177  1354.506442       7.136       7.415       1.127       1.135       0.000       0.000       0.000      10.838
## 178  1354.502934       6.984       7.416       1.127       1.136       0.000       0.000       0.000      10.836
## 179  1354.499445       6.834       7.417       1.127       1.136       0.000       0.000       0.000      10.834
## 180  1354.495975       6.685       7.418       1.127       1.136       0.000       0.000       0.000      10.831
## 181  1354.492525       6.539       7.419       1.127       1.136       0.000       0.000       0.000      10.829
## 182  1354.489097       6.395       7.420       1.127       1.136       0.000       0.000       0.000      10.826
## 183  1354.485691       6.252       7.420       1.127       1.136       0.000       0.000       0.000      10.824
## 184  1354.482308       6.112       7.421       1.127       1.136       0.000       0.000       0.000      10.822
## 185  1354.478950       5.973       7.422       1.127       1.136       0.000       0.000       0.000      10.819
## 186  1354.475616       5.837       7.422       1.127       1.137       0.000       0.000       0.000      10.817
## 187  1354.472309       5.703       7.423       1.127       1.137       0.000       0.000       0.000      10.814
## 188  1354.469029       5.570       7.423       1.127       1.137       0.000       0.000       0.000      10.812
## 189  1354.465776       5.440       7.423       1.127       1.137       0.000       0.000       0.000      10.809
## 190  1354.462552       5.311       7.423       1.127       1.137       0.000       0.000       0.000      10.807
## 191  1354.459358       5.185       7.424       1.127       1.137       0.000       0.000       0.000      10.805
## 192  1354.456195       5.061       7.424       1.127       1.137       0.000       0.000       0.000      10.802
## 193  1354.453062       4.939       7.424       1.127       1.137       0.000       0.000       0.000      10.800
## 194  1354.449962       4.819       7.424       1.127       1.137       0.000       0.000       0.000      10.797
## 195  1354.446895       4.700       7.424       1.127       1.138       0.000       0.000       0.000      10.795
## 196  1354.443862       4.584       7.424       1.127       1.138       0.000       0.000       0.000      10.792
## 197  1354.440863       4.470       7.424       1.127       1.138       0.000       0.000       0.000      10.790
## 198  1354.437899       4.358       7.423       1.127       1.138       0.000       0.000       0.000      10.788
## 199  1354.434971       4.248       7.423       1.127       1.138       0.000       0.000       0.000      10.785
## 200  1354.432079       4.140       7.423       1.127       1.138       0.000       0.000       0.000      10.783
## Timings:
## SpATS 22.454 seconds
## All process 23.063 seconds
## 
## Spatial analysis of trials with splines 
## 
## Response:                   variable  
## Genotypes (as random):      germplasm 
## Spatial:                    ~PSANOVA(col, row, nseg = c(nlevels(data_tmp$X), nlevels(data_tmp$Y)))
## Random:                     ~col_f + row_f
## 
## 
## Number of observations:        198
## Number of missing data:        13
## Effective dimension:           28.61
## Deviance:                      1354.432
## 
## Dimensions:
##                   Effective     Model     Nominal     Ratio     Type
## Intercept               1.0         1           1      1.00        F
## germplasm               4.1       184         183      0.02        R
## col_f                   7.4        54          52      0.14        R
## row_f                   1.1         4           2      0.56        R
## col                     1.0         1           1      1.00        S
## row                     1.0         1           1      1.00        S
## rowcol                  1.0         1           1      1.00        S
## f(col)                  1.1        55          55      0.02        S
## f(row)                  0.0         5           5      0.00        S
## f(col):row              0.0        55          55      0.00        S
## col:f(row)              0.0         5           5      0.00        S
## f(col):f(row)          10.8       275         275      0.04        S
##                                                                     
## Total                  28.6       641         636      0.04         
## Residual              169.4                                         
## Nobs                    198                                         
## 
## Type codes: F 'Fixed'    R 'Random'    S 'Smooth/Semiparametric'
## 
## 
## Spatial analysis of trials with splines 
## 
## Response:                   variable  
## Genotypes (as random):      germplasm 
## Spatial:                    ~PSANOVA(col, row, nseg = c(nlevels(data_tmp$X), nlevels(data_tmp$Y)))
## Random:                     ~col_f + row_f
## 
## 
## Number of observations:        198
## Number of missing data:        13
## Effective dimension:           28.61
## Deviance:                      1354.432
## 
## Dimensions:
##                   Effective     Model     Nominal     Ratio     Type
## Intercept               1.0         1           1      1.00        F
## germplasm               4.1       184         183      0.02        R
## col_f                   7.4        54          52      0.14        R
## row_f                   1.1         4           2      0.56        R
## col                     1.0         1           1      1.00        S
## row                     1.0         1           1      1.00        S
## rowcol                  1.0         1           1      1.00        S
## f(col)                  1.1        55          55      0.02        S
## f(row)                  0.0         5           5      0.00        S
## f(col):row              0.0        55          55      0.00        S
## col:f(row)              0.0         5           5      0.00        S
## f(col):f(row)          10.8       275         275      0.04        S
##                                                                     
## Total                  28.6       641         636      0.04         
## Residual              169.4                                         
## Nobs                    198                                         
## 
## Type codes: F 'Fixed'    R 'Random'    S 'Smooth/Semiparametric'

out_spatial is a list containing two elements :

info : a list with variable and data

out_spatial$info$variable

## [1] "y1"

head(out_spatial$info$data)

##                   seed_lot location year germplasm block X Y    y1
## 1   germ-1_loc-1_2018_0001    loc-1 2018    germ-1     1 1 1 36.20
## 2 germ-108_loc-1_2018_0001    loc-1 2018  germ-108     1 2 1 38.55
## 3 germ-119_loc-1_2018_0001    loc-1 2018  germ-119     1 3 1 38.80
## 4 germ-130_loc-1_2018_0001    loc-1 2018  germ-130     1 4 1    NA
## 5 germ-118_loc-1_2018_0001    loc-1 2018  germ-118     1 5 1 48.00
## 6 germ-120_loc-1_2018_0001    loc-1 2018  germ-120     1 6 1 78.85

model a list with four elements :

model

out_spatial$model$model

## 
## Spatial analysis of trials with splines 
## 
## Response:                   variable  
## Genotypes (as random):      germplasm 
## Spatial:                    ~PSANOVA(col, row, nseg = c(nlevels(data_tmp$X), nlevels(data_tmp$Y)))
## Random:                     ~col_f + row_f
## 
## 
## Number of observations:        198
## Number of missing data:        13
## Effective dimension:           28.61
## Deviance:                      1354.432

summary

out_spatial$model$summary

## 
## Spatial analysis of trials with splines 
## 
## Response:                   variable  
## Genotypes (as random):      germplasm 
## Spatial:                    ~PSANOVA(col, row, nseg = c(nlevels(data_tmp$X), nlevels(data_tmp$Y)))
## Random:                     ~col_f + row_f
## 
## 
## Number of observations:        198
## Number of missing data:        13
## Effective dimension:           28.61
## Deviance:                      1354.432
## 
## Dimensions:
##                   Effective     Model     Nominal     Ratio     Type
## Intercept               1.0         1           1      1.00        F
## germplasm               4.1       184         183      0.02        R
## col_f                   7.4        54          52      0.14        R
## row_f                   1.1         4           2      0.56        R
## col                     1.0         1           1      1.00        S
## row                     1.0         1           1      1.00        S
## rowcol                  1.0         1           1      1.00        S
## f(col)                  1.1        55          55      0.02        S
## f(row)                  0.0         5           5      0.00        S
## f(col):row              0.0        55          55      0.00        S
## col:f(row)              0.0         5           5      0.00        S
## f(col):f(row)          10.8       275         275      0.04        S
##                                                                     
## Total                  28.6       641         636      0.04         
## Residual              169.4                                         
## Nobs                    198                                         
## 
## Type codes: F 'Fixed'    R 'Random'    S 'Smooth/Semiparametric'

var_res the variance of the residuals

out_spatial$model$df_residual

## [1] 169.4

out_spatial$model$MSerror

## [1] 7.995467

3.5.4.5 Check and visualize model outputs

The tests to check the model are explained in section 3.1.2.1.2.

3.5.4.5.1 Check the model

out_check_spatial = check_model(out_spatial)

out_check_spatial is a list containing two elements :

spatial the output from the model
data_ggplot a list containing information for ggplot:
- data_ggplot_residuals a list containing :
  - data_ggplot_normality
  - data_ggplot_skewness_test
  - data_ggplot_kurtosis_test
  - data_ggplot_qqplot
- data_ggplot_variability_repartition_pie

3.5.4.5.2 Visualize outputs

Once the computation is done, you can visualize the results with plot

p_out_check_spatial = plot(out_check_spatial)

p_out_check_spatial is a list with:

residuals

histogram : histogram with the distribution of the residuals

p_out_check_spatial$residuals$histogram

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.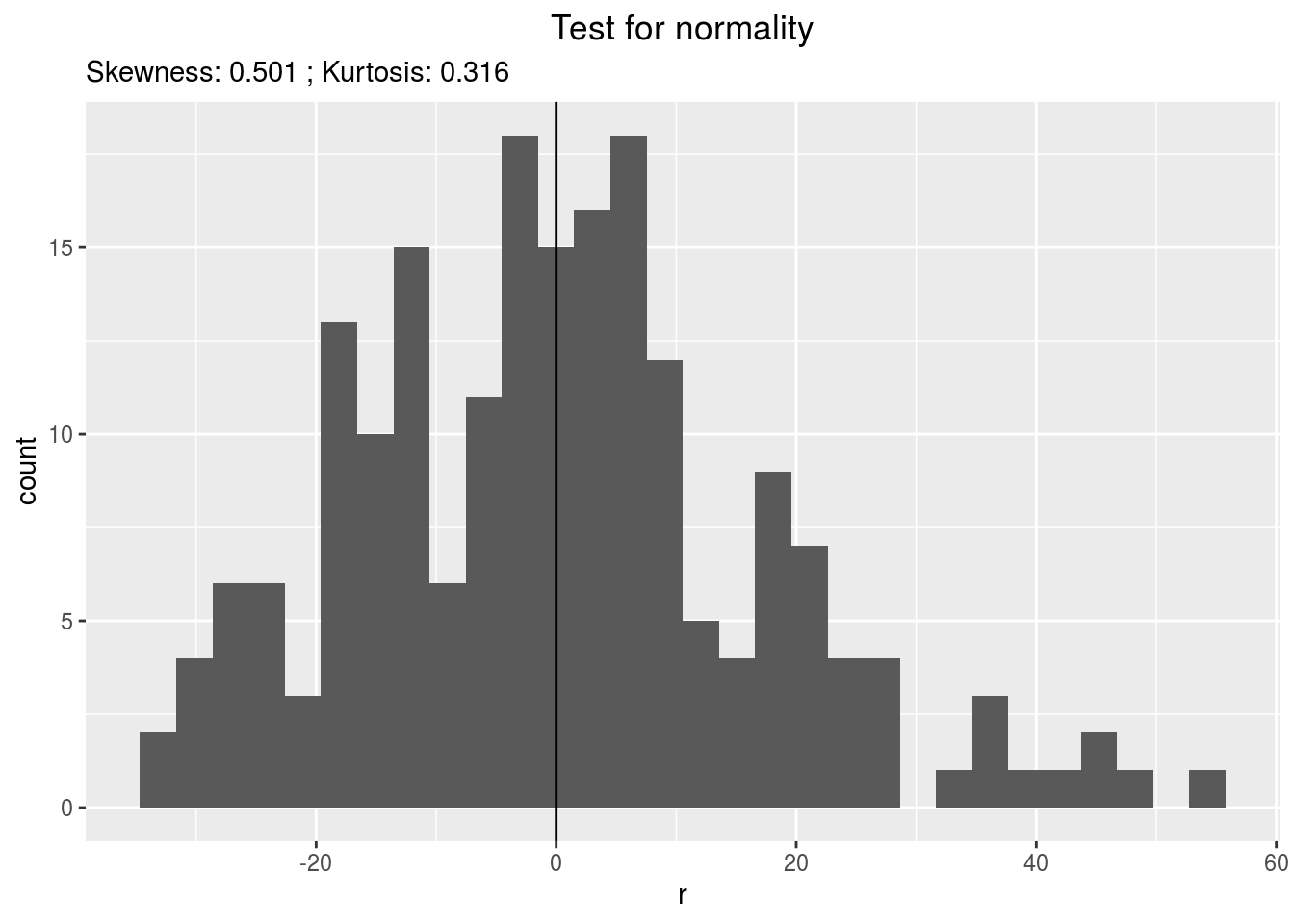

qqplot

p_out_check_spatial$residuals$qqplot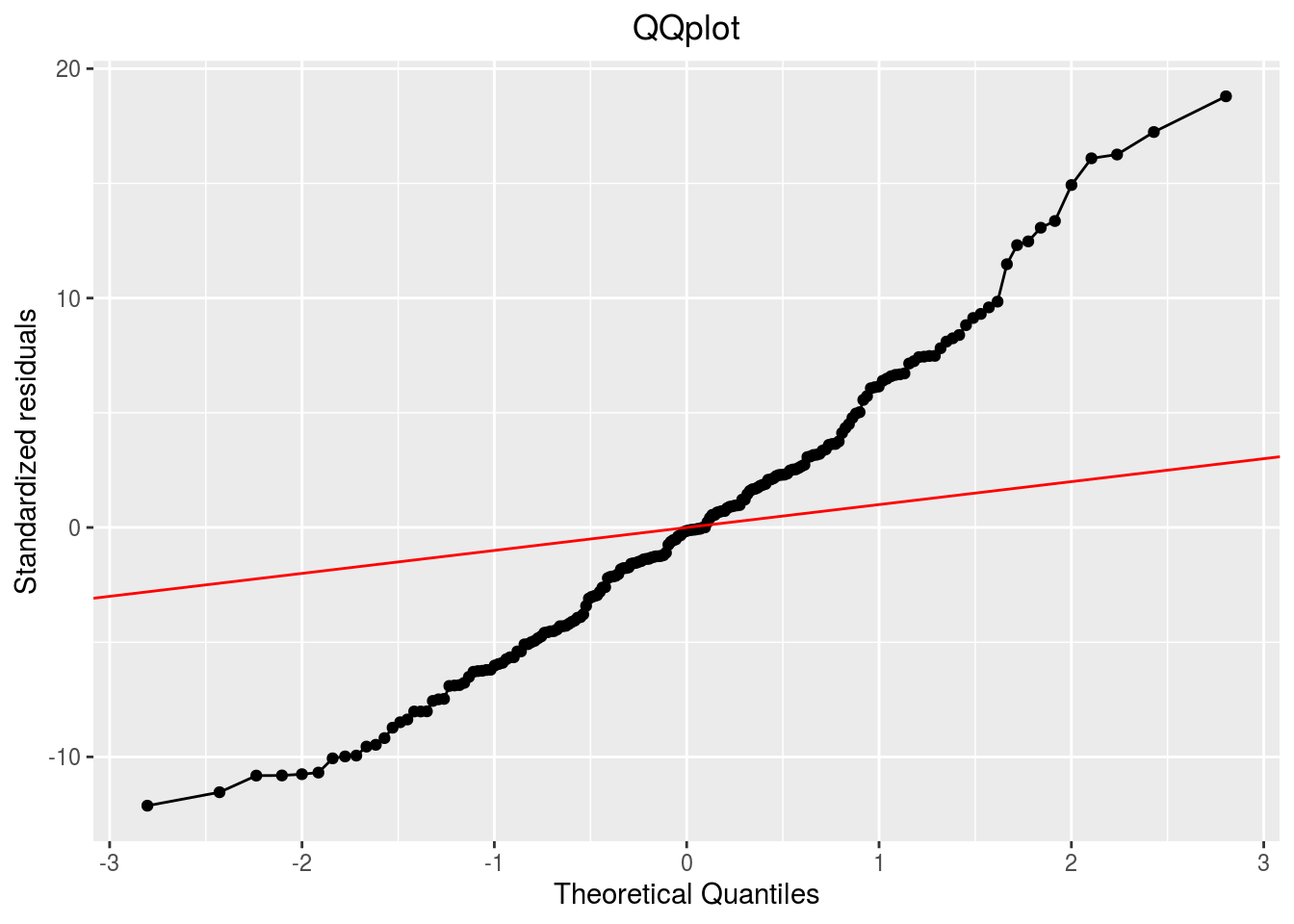

variability_repartition : pie with repartition of variance for each factor

p_out_check_spatial$variability_repartition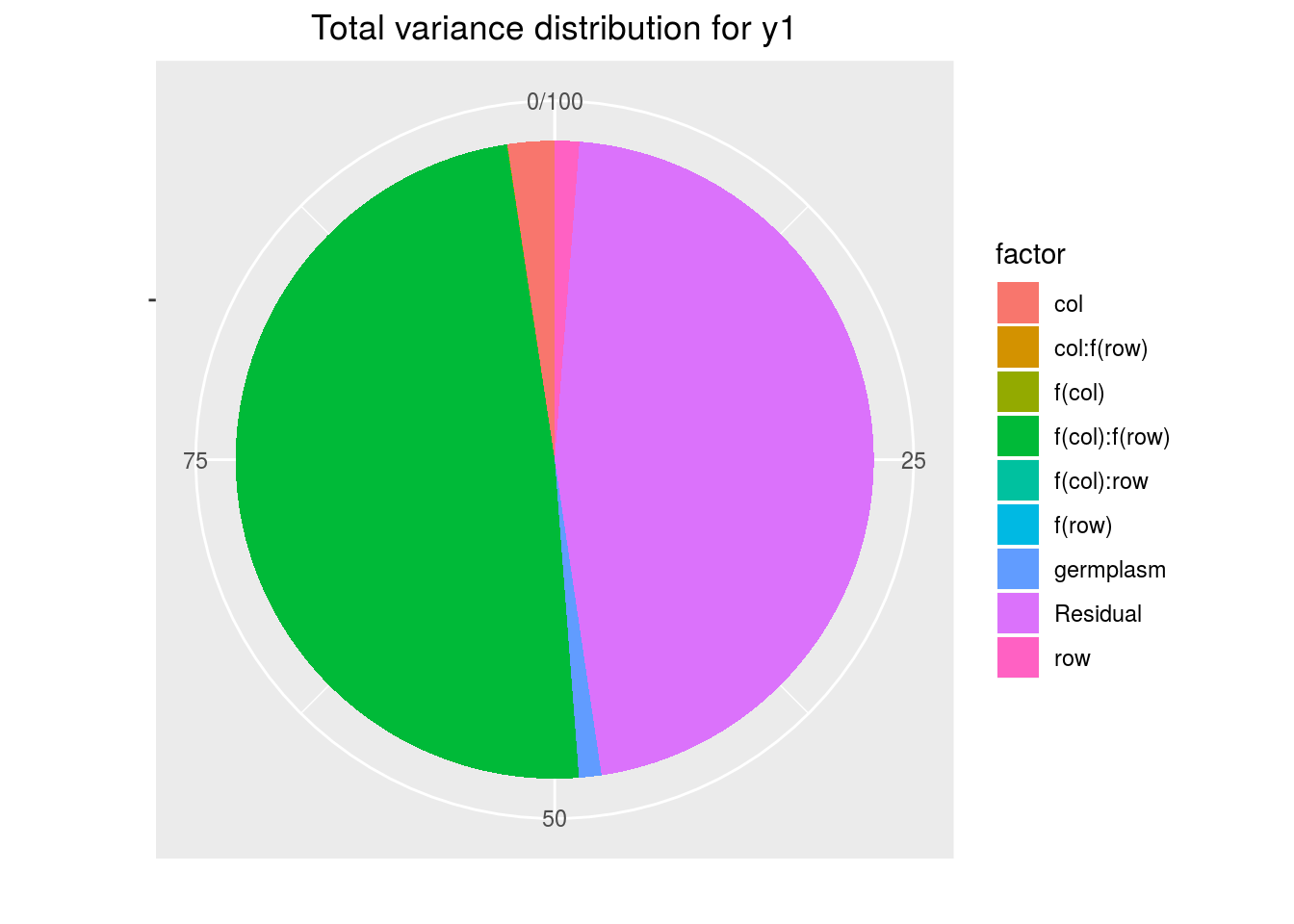

3.5.4.6 Get and visualize mean comparisons

The method to compute mean comparison are explained in section 3.1.2.1.3.

3.5.4.7 Get mean comparisons

Get mean comparisons with mean_comparisons.

out_mean_comparisons_spatial = mean_comparisons(out_check_spatial, p.adj = "bonferroni")

out_mean_comparisons_spatial is a list of two elements:

info : a list with variable and data
data_ggplot_LSDbarplot_germplasm

3.5.4.8 Visualize mean comparisons

p_out_mean_comparisons_spatial = plot(out_mean_comparisons_spatial)

p_out_mean_comparisons_spatial is a list of two elements

germplasm_blup whih represent the BLUPs with their confidence intervalle

p_out_mean_comparisons_spatial$germplasm_blup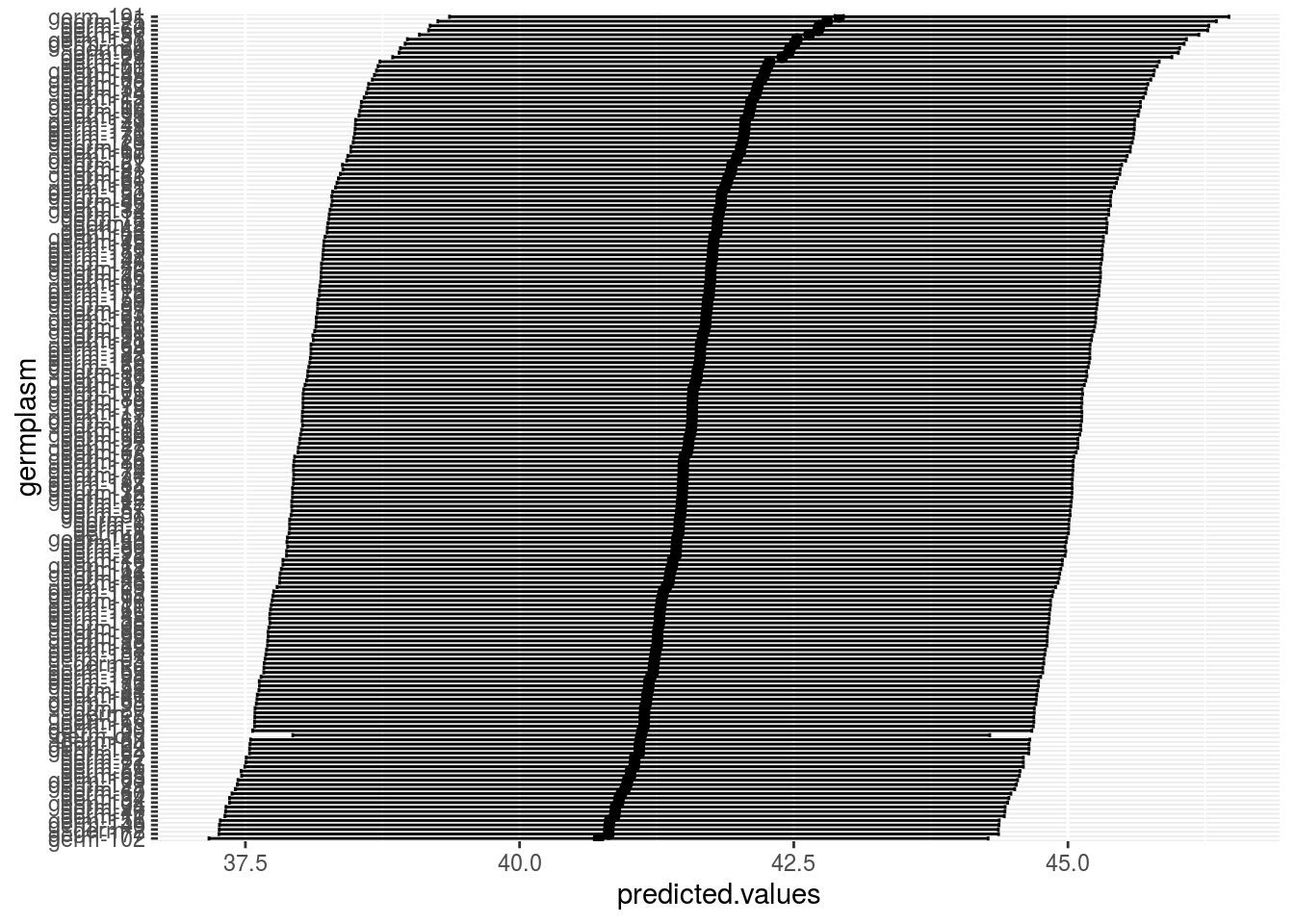

germplasm_barplot. For each element of the list, there are as many graph as needed with nb_parameters_per_plot parameters per graph. Letters are displayed on each bar. Parameters that do not share the same letters are different regarding type I error (alpha) and alpha correction. The error I (alpha) and the alpha correction are displayed in the title.

pg = p_out_mean_comparisons_spatial$germplasm_barplot
pg$`23`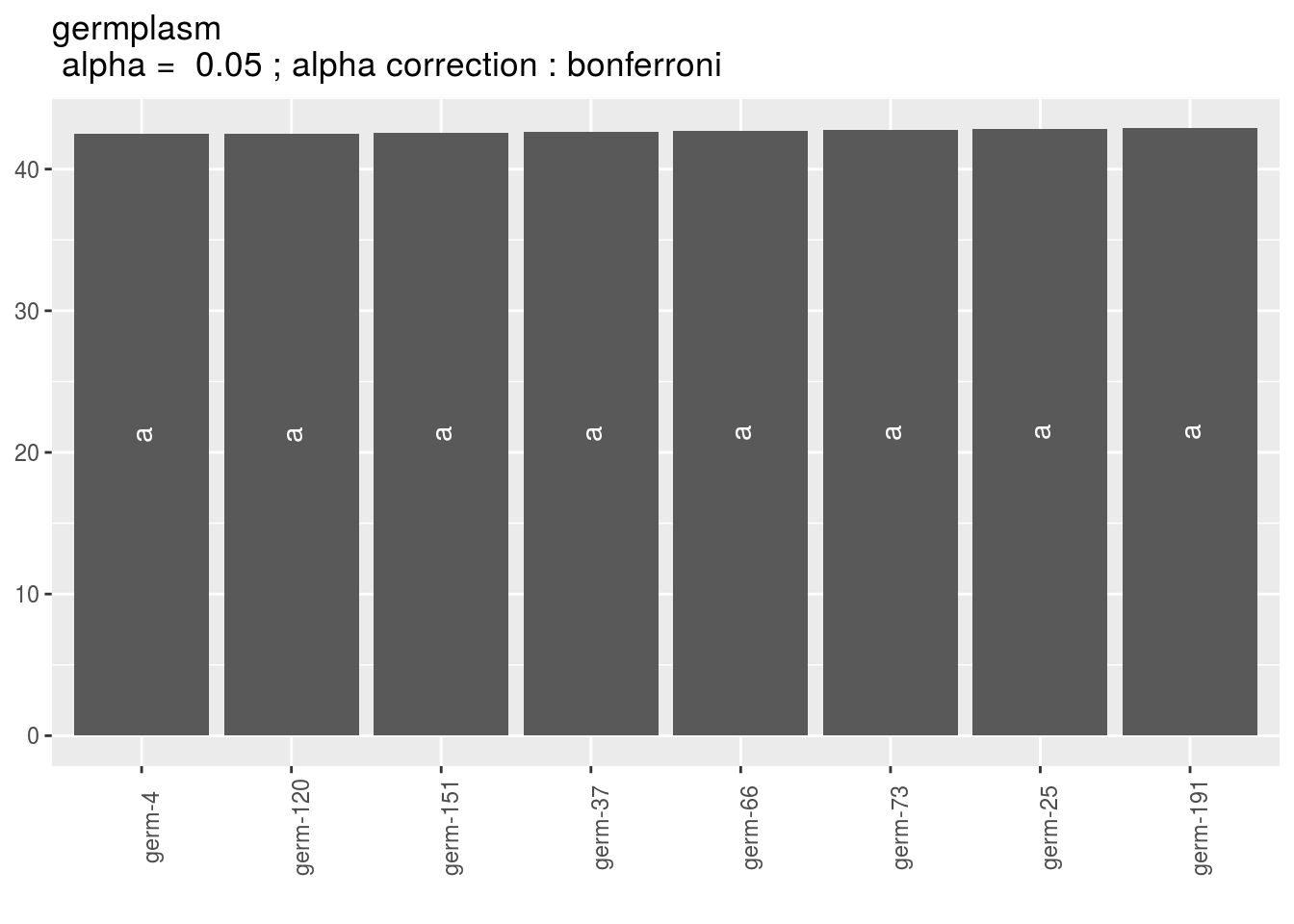

3.5.4.9 Apply the workflow to several variables

If you wish to apply the spatial workflow to several variables, you can use lapply with the following code :

workflow_spatial = function(x, data){
  out_spatial = model_spatial(data = data, variable = x)
  
  out_check_spatial = check_model(out_spatial)
  p_out_check_spatial = plot(out_check_spatial)
  
  out_mean_comparisons_spatial = mean_comparisons(out_check_spatial, p.adj = "bonferroni")
  p_out_mean_comparisons_spatial = plot(out_mean_comparisons_spatial)
  
  out = list(
    out_spatial = out_spatial,
    out_check_spatial = out_check_spatial,
    p_out_check_spatial = p_out_check_spatial,
    out_mean_comparisons_spatial = out_mean_comparisons_spatial,
    p_out_mean_comparisons_spatial = p_out_mean_comparisons_spatial
    )
  return(out)
}

## Not run 
# vec_variables = c("y1", "y2", "y3")
#
# out = lapply(vec_variables, workflow_spatial, data)
# names(out) = vec_variables

3.5.5 Mixted model for incomplete block design (M5)

!!! TO DO !!!

The model is based on frequentist statistics (section 3.1.2.1). The tests to check the model are explained in section 3.1.2.1.2. The method to compute mean comparison are explained in section 3.1.2.1.3.

(Zystro, Colley, and Dawson 2018)

#library(ibd)
#data(ibddata)
#aov.ibd(y~factor(trt)+factor(blk),data=ibddata)
#contrast=matrix(c(1,-1,0,0,0,0,0,0,0,0,0,1,-1,0,0,0,0,0),nrow=2,byrow=TRUE)
#aov.ibd(y~factor(trt)+factor(blk),specs="trt",data=ibddata,contrast=contrast)

3.5.6 Hierarchical Bayesian intra-location model to perform mean comparisons with each farm (M7a)

At the farm level, the residual has few degrees of freedom, leading to a poor estimation of the residual variance and to a lack of power for comparing populations. model_bh_intra_location was implemented to improve efficiency of mean comparisons. It is efficient with more than 20 environment (i.e. location \(\times\) year) (Rivière et al. 2015). The model is based on bayesian statistics (section 3.1.2.2).

3.5.6.1 Theory of the model

The experimental design used is satellite and regional farms (D4). The model is described in Rivière et al. (2015). We restricted ourselves to analysing values at the plot level (the values may result from the average of individual plants measures). The phenotypic value \(Y_{ijk}\) for variable \(Y\), germplasm \(i\), environment \(j\) and block \(k\) is modelled as :

\(Y_{ijk} = \mu_{ij} + \beta_{jk} + \varepsilon_{ijk} ; \quad \varepsilon_{ijk} \sim \mathcal{N} (0,\sigma^2_{j})\),

where

\(\mu_{ij}\) is the mean of germplasm \(i\) in environment \(j\) (note that this parameter, which corresponds to an entry, confounds the population effect and the population \(\times\) environment effect);
\(\beta_{jk}\) is the effect of block \(k\) in environment \(j\) satisfying the constraint⁹ \(\sum\limits_{k=1}^K \beta_{jk} = 1\) ;
\(\varepsilon_{ijk}\) is the residual error;
\(\mathcal{N} (0,\sigma^2_{j})\) denotes normal distribution centred on 0 with variance \(\sigma^2_{j}\), which is specific to environment \(j\).

We take advantage of the similar structure of the trials in each environment of the network to assume that trial residual variances come from a common distribution :

\(\sigma^2_{j} \sim \frac{1}{Gamma(\nu,\rho)}\),

where \(\nu\) and \(\rho\) are unknown parameters. Because of the low number of residual degrees of freedom for each farm, we use a hierarchical approach in order to assess mean differences on farm. For that, we place vague prior distributions on the hyperparameters \(\nu\) and \(\rho\) :

\(\nu \sim Uniform(\nu_{min},\nu_{max}) ; \quad \rho \sim Gamma(10^{-6},10^{-6})\).

In other words, the residual variance of a trial in a given environment is estimated using all the informations available on the network rather than using the data from that particular trial only.

The parameters \(\mu_{ij}\) and \(\beta_{jk}\) are assumed to follow vague prior distributions too:

\(\mu_{ij} \sim \mathcal{N}(\mu_{.j},10^{6}); \quad \beta_{jk} \sim \mathcal{N}(0,10^{6})\).

The inverse gamma distribution has a minimum value of 0 (consistent with the definition of a variance) and may have various shapes including asymmetric distributions. From an agronomical point of view, the assumption that trial variances are heterogeneous is consistent with organic farming: there are as many environments as farms and farmers leading to a high heterogeneity. Environment is here considered in a broad sense: practices (sowing date, sowing density, tilling, etc.), pedo climatic conditions, biotic and abiotic stress, … (Desclaux et al. 2008). Moreover, the inverse gamma distribution has conjugate properties that facilitate MCMC convergence. This model is therefore a good choice based on both agronomic and statistical criteria.

The residual variance estimated from the controls is assumed to be representative of the residual variance of the other entries. Blocks are included in the model only if the trial has blocks.

3.5.6.2 Steps with

To run model_bh_intra_location, follow these steps (Figure 3.2):

Format the data with format_data_PPBstats()
Run the model with model_bh_intra_location()
Check model outputs with graphs using check_model()to know if you can continue the analysis
Get mean comparisons for each factor with mean_comparisons() and vizualise it with plot()

3.5.6.3 Format the data

The values for \(\mu_{ij}\), \(\beta_{jk}\), \(\epsilon_{ijk}\) and \(\sigma_j\) are the real value used to create the simulated dataset. This dataset is representative of data obtain in a PPB programme.

data(data_model_bh_intra_location)
data_model_bh_intra_location = format_data_PPBstats(data_model_bh_intra_location, type = "data_agro")

## Warning in format_data_PPBstats.data_agro(data): Column "long" is needed to
## get map and not present in data.

## Warning in format_data_PPBstats.data_agro(data): Column "lat" is needed to
## get map and not present in data.

## data has been formated for PPBstats functions.

head(data_model_bh_intra_location) # first rows of the data

##                  seed_lot location year germplasm block X Y      tkw
## 1 germ-25_loc-1_2005_0001    loc-1 2005   germ-25     1 1 a 72.09900
## 2 germ-26_loc-1_2005_0001    loc-1 2005   germ-26     1 2 b 61.05274
## 3 germ-27_loc-1_2005_0001    loc-1 2005   germ-27     1 3 c 62.99350
## 4 germ-28_loc-1_2005_0001    loc-1 2005   germ-28     1 4 d 65.10909
## 5 germ-25_loc-1_2005_0001    loc-1 2005   germ-25     2 5 e 77.01361
## 6 germ-26_loc-1_2005_0001    loc-1 2005   germ-26     2 6 f 64.10541
##     tkw$date    mu_ij beta_jk epsilon_ijk  sigma_j tkw$date_julian
## 1 2017-07-22 73.37224       0  -1.2732421 1.622339             202
## 2 2017-07-22 61.61823       0  -0.5654918 1.622339             202
## 3 2017-07-22 64.31830       0  -1.3248006 1.622339             202
## 4 2017-07-22 62.57840       0   2.5306946 1.622339             202
## 5 2017-07-22 73.37224       0   3.6413666 1.622339             202
## 6 2017-07-22 61.61823       0   2.4871807 1.622339             202

3.5.6.4 Run the model

To run model model_bh_intra_location on the dataset, used the function model_bh_intra_location(). Here it is run on thousand kernel weight (tkw).

By default, model_bh_intra_location returns posteriors for \(\mu_{ij}\) (return.mu = TRUE), \(\beta_{jk}\) (return.beta = TRUE), \(\sigma_j\) (return.sigma = TRUE), \(\nu\) (return.nu = TRUE) and \(\rho\) (return.rho = TRUE). You can also get \(\epsilon_{ijk}\) value with return.espilon = TRUE.

DIC criterion is a generalization of the AIC criterion that can be used for hierarchical models (Spiegelhalter et al. 2002). The smaller the DIC value, the better the model (Plummer 2008). By default, DIC is not displayed, you can ask for this value to compare to other model (DIC = TRUE).

# out_model_bh_intra_location = model_bh_intra_location(data = data_model_bh_intra_location, variable = "tkw", return.epsilon = TRUE)

# Compiling model graph
# Resolving undeclared variables
# Allocating nodes
# Graph information:
#   Observed stochastic nodes: 976
# Unobserved stochastic nodes: 927
# Total graph size: 8609
# 
# Initializing model
# 
# |++++++++++++++++++++++++++++++++++++++++++++++++++| 100%
# |**************************************************| 100%
# |**************************************************| 100%
# |**************************************************| 100%

load("./data_PPBstats/out_model_bh_intra_location.RData") # To save time

You can get information on the environments in the dataset :

out_model_bh_intra_location$vec_env_with_no_data

## NULL

out_model_bh_intra_location$vec_env_with_no_controls

## [1] "loc-25:2005"

out_model_bh_intra_location$vec_env_with_controls

##  [1] "loc-10:2005" "loc-10:2006" "loc-10:2007" "loc-11:2005" "loc-11:2006"
##  [6] "loc-11:2007" "loc-1:2005"  "loc-1:2006"  "loc-1:2007"  "loc-12:2005"
## [11] "loc-12:2006" "loc-12:2007" "loc-13:2005" "loc-13:2006" "loc-13:2007"
## [16] "loc-14:2005" "loc-14:2006" "loc-14:2007" "loc-15:2005" "loc-15:2006"
## [21] "loc-15:2007" "loc-16:2005" "loc-16:2006" "loc-16:2007" "loc-17:2005"
## [26] "loc-17:2006" "loc-17:2007" "loc-18:2005" "loc-18:2006" "loc-18:2007"
## [31] "loc-19:2006" "loc-19:2007" "loc-20:2006" "loc-20:2007" "loc-21:2006"
## [36] "loc-21:2007" "loc-2:2005"  "loc-2:2006"  "loc-2:2007"  "loc-22:2006"
## [41] "loc-22:2007" "loc-23:2006" "loc-23:2007" "loc-3:2005"  "loc-3:2006" 
## [46] "loc-3:2007"  "loc-4:2005"  "loc-4:2006"  "loc-4:2007"  "loc-5:2006" 
## [51] "loc-6:2006"  "loc-6:2007"  "loc-7:2006"  "loc-7:2007"  "loc-8:2006" 
## [56] "loc-9:2005"  "loc-9:2006"  "loc-9:2007"

out_model_bh_intra_location$vec_env_RF

##  [1] "loc-1:2005" "loc-1:2006" "loc-1:2007" "loc-2:2005" "loc-2:2006"
##  [6] "loc-2:2007" "loc-3:2005" "loc-3:2006" "loc-3:2007" "loc-4:2005"
## [11] "loc-4:2006" "loc-4:2007" "loc-5:2006" "loc-6:2006" "loc-6:2007"
## [16] "loc-7:2006" "loc-7:2007" "loc-8:2006"

out_model_bh_intra_location$vec_env_SF

##  [1] "loc-10:2005" "loc-10:2006" "loc-10:2007" "loc-11:2005" "loc-11:2006"
##  [6] "loc-11:2007" "loc-12:2005" "loc-12:2006" "loc-12:2007" "loc-13:2005"
## [11] "loc-13:2006" "loc-13:2007" "loc-14:2005" "loc-14:2006" "loc-14:2007"
## [16] "loc-15:2005" "loc-15:2006" "loc-15:2007" "loc-16:2005" "loc-16:2006"
## [21] "loc-16:2007" "loc-17:2005" "loc-17:2006" "loc-17:2007" "loc-18:2005"
## [26] "loc-18:2006" "loc-18:2007" "loc-19:2006" "loc-19:2007" "loc-20:2006"
## [31] "loc-20:2007" "loc-21:2006" "loc-21:2007" "loc-22:2006" "loc-22:2007"
## [36] "loc-23:2006" "loc-23:2007" "loc-9:2005"  "loc-9:2006"  "loc-9:2007"

Below is an example with low nb_iterations (see section 3.1.2.2 about the number of iterations):

# out_model_bh_intra_location_bis = model_bh_intra_location(data = data_model_bh_intra_location, variable = "tkw", nb_iteration = 5000)

# Compiling model graph
# Resolving undeclared variables
# Allocating nodes
# Graph information:
#   Observed stochastic nodes: 976
# Unobserved stochastic nodes: 927
# Total graph size: 8609
# 
# Initializing model
# 
# |++++++++++++++++++++++++++++++++++++++++++++++++++| 100%
# |**************************************************| 100%
# |**************************************************| 100%
# Warning message:
#   In model_bh_intra_location(data = data_model_bh_intra_location, variable = "tkw", nb_iteration = 5000) :
#   nb_iterations is below 20 000, which seems small to get convergence in the MCMC.

load("./data_PPBstats/out_model_bh_intra_location_bis.RData") # To save time

3.5.6.5 Check and visualize model outputs

The tests to check the model are explained in section 3.1.2.2.2.

3.5.6.5.1 Check the model

Once the model has been run, it is necessary to check if the outputs can be taken with confidence. This step is needed before going ahead in the analysis (in fact the object used in the next functions must come from check_model).

# out_check_model_bh_intra_location = check_model(out_model_bh_intra_location)

# The Gelman-Rubin test is running for each parameter ...
# The two MCMC for each parameter converge thanks to the Gelman-Rubin test.

load("./data_PPBstats/out_check_model_bh_intra_location.RData") # To save time

out_check_model_bh_intra_location is a list containing:

MCMC : a data fame resulting from the concatenation of the two MCMC for each parameter. This object can be used for further analysis. There are as many columns as parameters and as many rows as iterations/thin (the thin value is 10 by default in the models).

dim(out_check_model_bh_intra_location$MCMC)

## [1] 20000   945

MCMC_conv_not_ok: a data fame resulting from the concatenation of the two MCMC for each parameter for environments where some parameters did not converge for mu and beta
data_env_with_no_controls : data frame with environnements without controls
data_env_whose_param_did_not_converge : a list with data frame with environments where some parameters did not converge for mu and beta
data_ggplot : a list containing information for ggplot:
- sigma_j
- mu_ij
- beta_jk
- sigma_j_2
- epsilon_ijk

When considering out_model_bh_intra_location_bis:

# out_check_model_bh_intra_location_bis = check_model(out_model_bh_intra_location_bis)

# The Gelman-Rubin test is running for each parameter ...
# The two MCMC of the following parameters do not converge thanks to the Gelman-Rubin test : # mu[germ-20,loc-15:2006], nu, rho, sigma[loc-15:2006]. Therefore, they are not present in MCMC output.
# MCMC are updated, the following environment were deleted : loc-15:2006
# data_env_whose_param_did_not_converge contains the raw data for these environments.

load("./data_PPBstats/out_check_model_bh_intra_location_bis.RData") # To save time

3.5.6.5.2 Visualize outputs

Once the computation is finished, you can visualize the results with

p_out_check_model_bh_intra_location = plot(out_check_model_bh_intra_location)

## Distribution of sigma_j in the inverse Gamme distribution are done.

## The mu_ij posterior distributions are done.

## The beta_jk posterior distributions are done.

## The sigma_j posterior distributions are done.

## The standardised residuals distributions are done.

p_out_check_model_bh_intra_location is a list with:

sigma_j_gamma : mean of each sigma_j displayed on the Inverse Gamma distribution. The first graph represents all the sigma_j, the other graph represent the same information divided into several graphs (based on argument nb_parameters_per_plot).

p_out_check_model_bh_intra_location$sigma_j_gamma[[1]]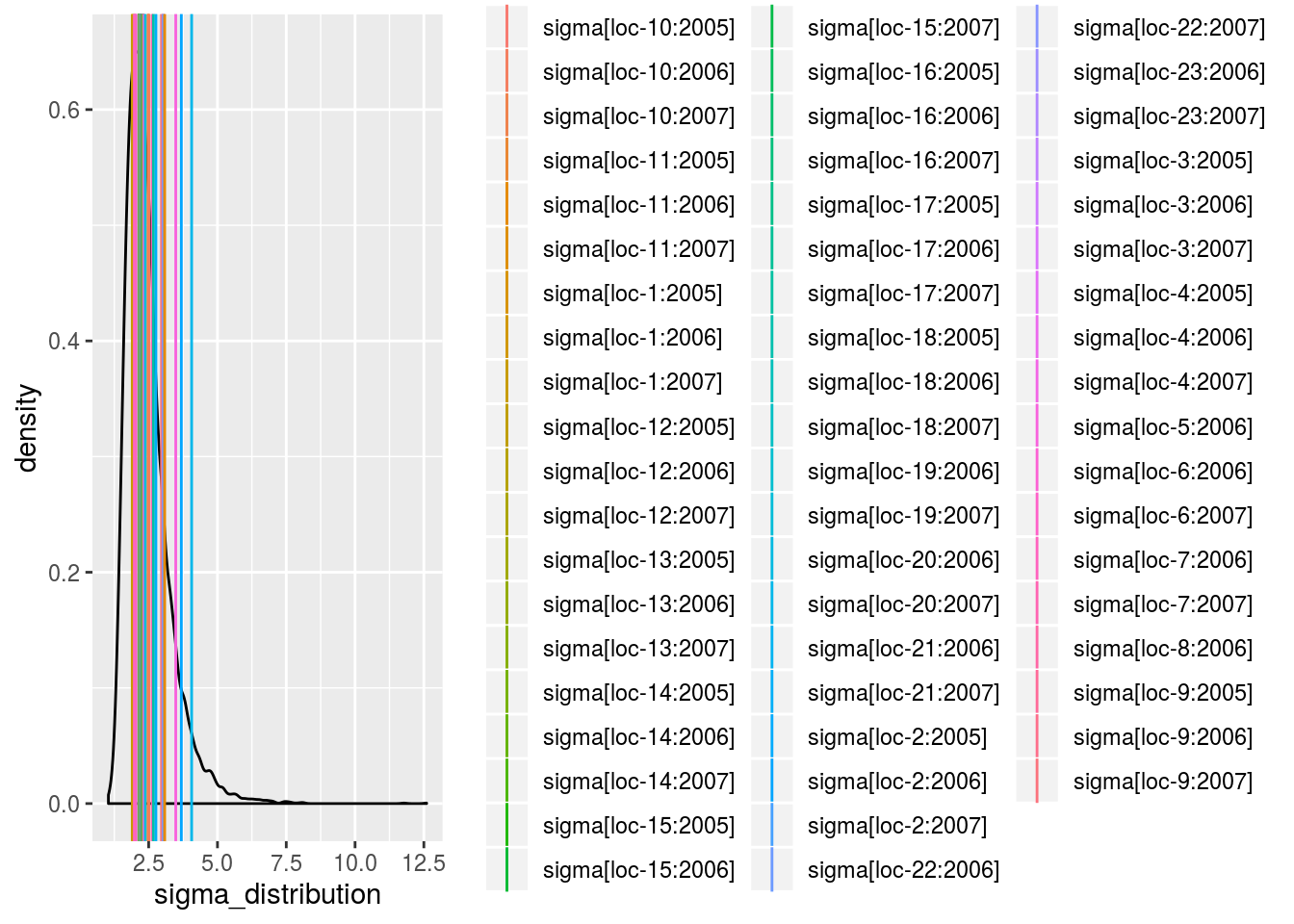

p_out_check_model_bh_intra_location$sigma_j_gamma[[2]]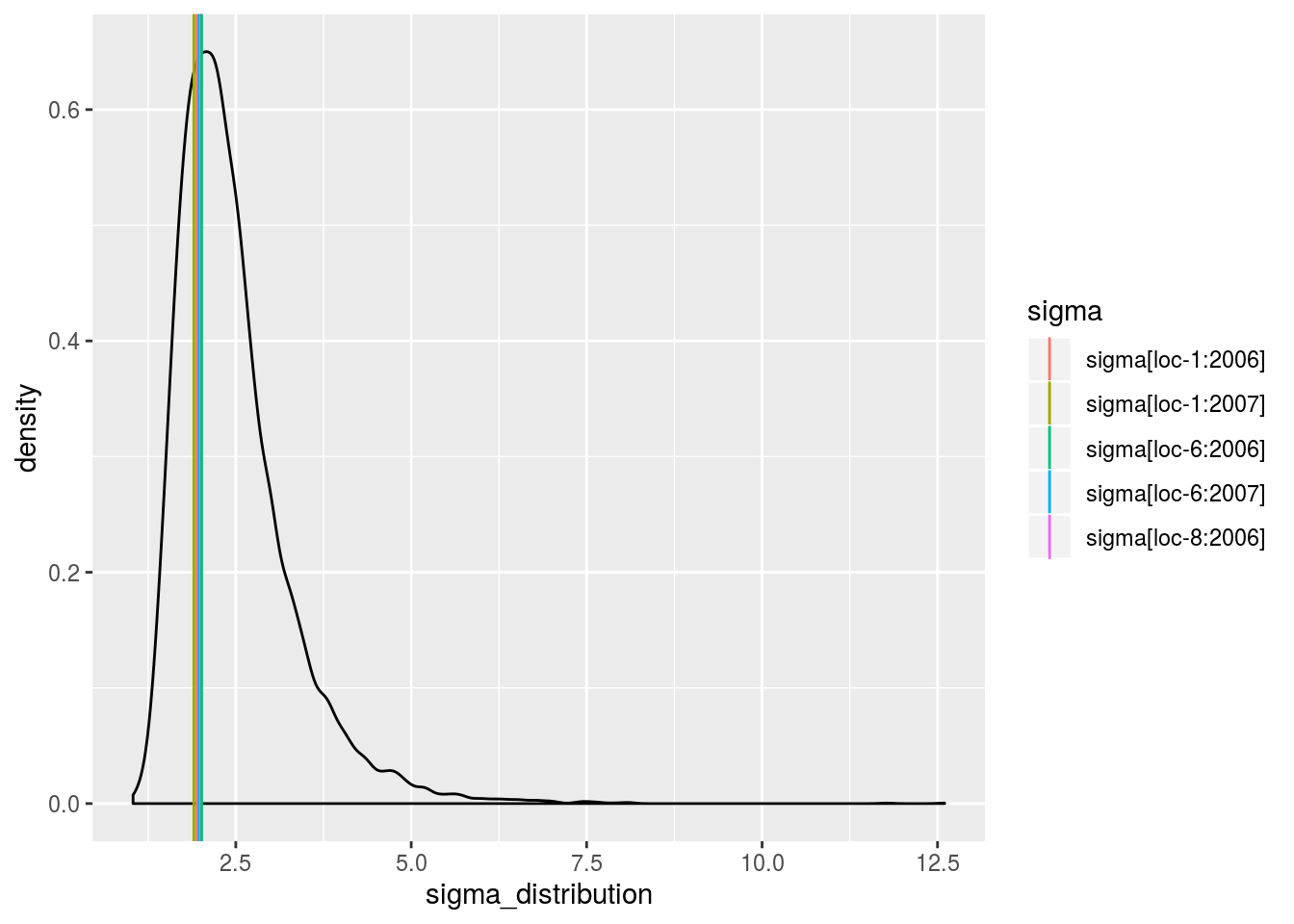

mu_ij : distribution of each mu_ij in a list with as many elements as environment. For each element of the list, there are as many graph as needed with nb_parameters_per_plot mu_ij per graph.

names(p_out_check_model_bh_intra_location$mu_ij)

##  [1] "loc-10:2005" "loc-10:2006" "loc-10:2007" "loc-11:2005" "loc-11:2006"
##  [6] "loc-11:2007" "loc-1:2005"  "loc-1:2006"  "loc-1:2007"  "loc-12:2005"
## [11] "loc-12:2006" "loc-12:2007" "loc-13:2005" "loc-13:2006" "loc-13:2007"
## [16] "loc-14:2005" "loc-14:2006" "loc-14:2007" "loc-15:2005" "loc-15:2006"
## [21] "loc-15:2007" "loc-16:2005" "loc-16:2006" "loc-16:2007" "loc-17:2005"
## [26] "loc-17:2006" "loc-17:2007" "loc-18:2005" "loc-18:2006" "loc-18:2007"
## [31] "loc-19:2006" "loc-19:2007" "loc-20:2006" "loc-20:2007" "loc-21:2006"
## [36] "loc-21:2007" "loc-2:2005"  "loc-2:2006"  "loc-2:2007"  "loc-22:2006"
## [41] "loc-22:2007" "loc-23:2006" "loc-23:2007" "loc-3:2005"  "loc-3:2006" 
## [46] "loc-3:2007"  "loc-4:2005"  "loc-4:2006"  "loc-4:2007"  "loc-5:2006" 
## [51] "loc-6:2006"  "loc-6:2007"  "loc-7:2006"  "loc-7:2007"  "loc-8:2006" 
## [56] "loc-9:2005"  "loc-9:2006"  "loc-9:2007"

names(p_out_check_model_bh_intra_location$mu_ij$`loc-10:2005`)

## [1] "1"

p_out_check_model_bh_intra_location$mu_ij$`loc-10:2005`$`1`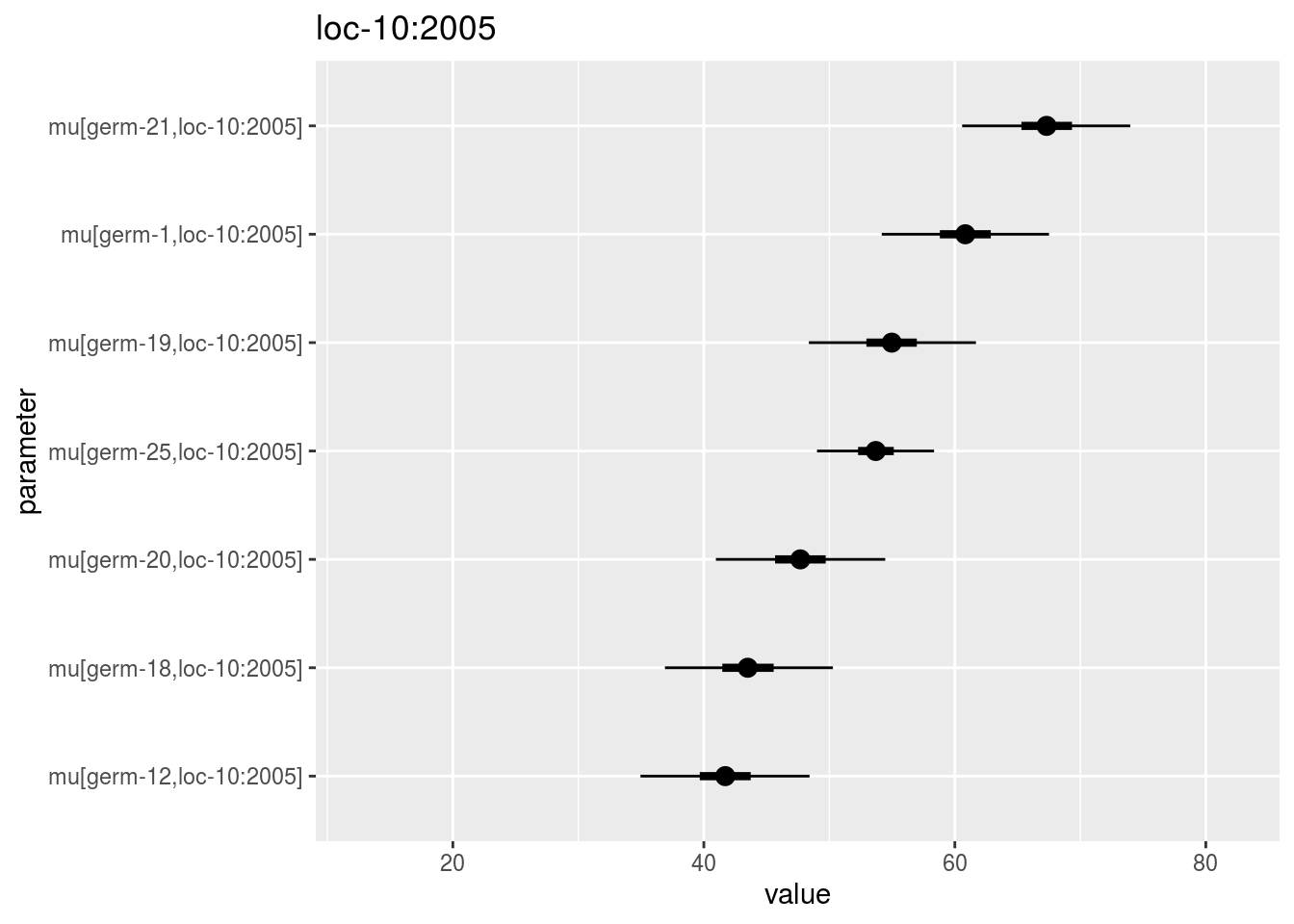

beta_jk : distribution of each beta_jk in a list with as many elements as environment. For each element of the list, there are as many graph as needed with nb_parameters_per_plot beta_jk per graph.

names(p_out_check_model_bh_intra_location$beta_jk)

##  [1] "loc-1:2005" "loc-1:2006" "loc-1:2007" "loc-2:2005" "loc-2:2006"
##  [6] "loc-2:2007" "loc-3:2005" "loc-3:2006" "loc-3:2007" "loc-4:2005"
## [11] "loc-4:2006" "loc-4:2007" "loc-5:2006" "loc-6:2006" "loc-6:2007"
## [16] "loc-7:2006" "loc-7:2007" "loc-8:2006"

names(p_out_check_model_bh_intra_location$beta_jk$`loc-1:2005`)

## [1] "1"

p_out_check_model_bh_intra_location$beta_jk$`loc-1:2005`$`1`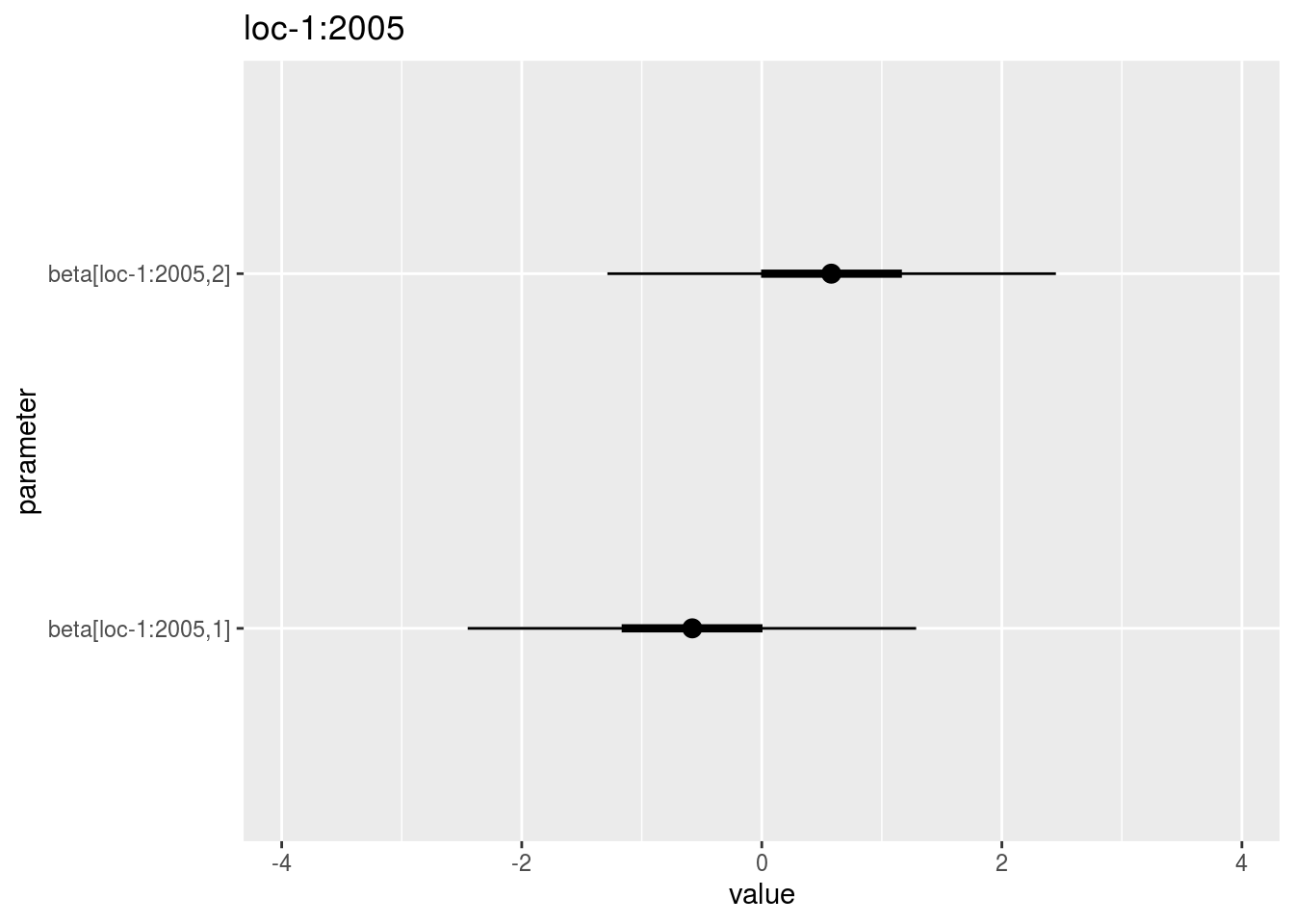

sigma_j : distribution of each sigma_j. There are as many graph as needed with nb_parameters_per_plot sigma_j per graph.

names(p_out_check_model_bh_intra_location$sigma_j)

## [1] "1" "2" "3" "4" "5" "6" "7" "8"

p_out_check_model_bh_intra_location$sigma_j[[1]]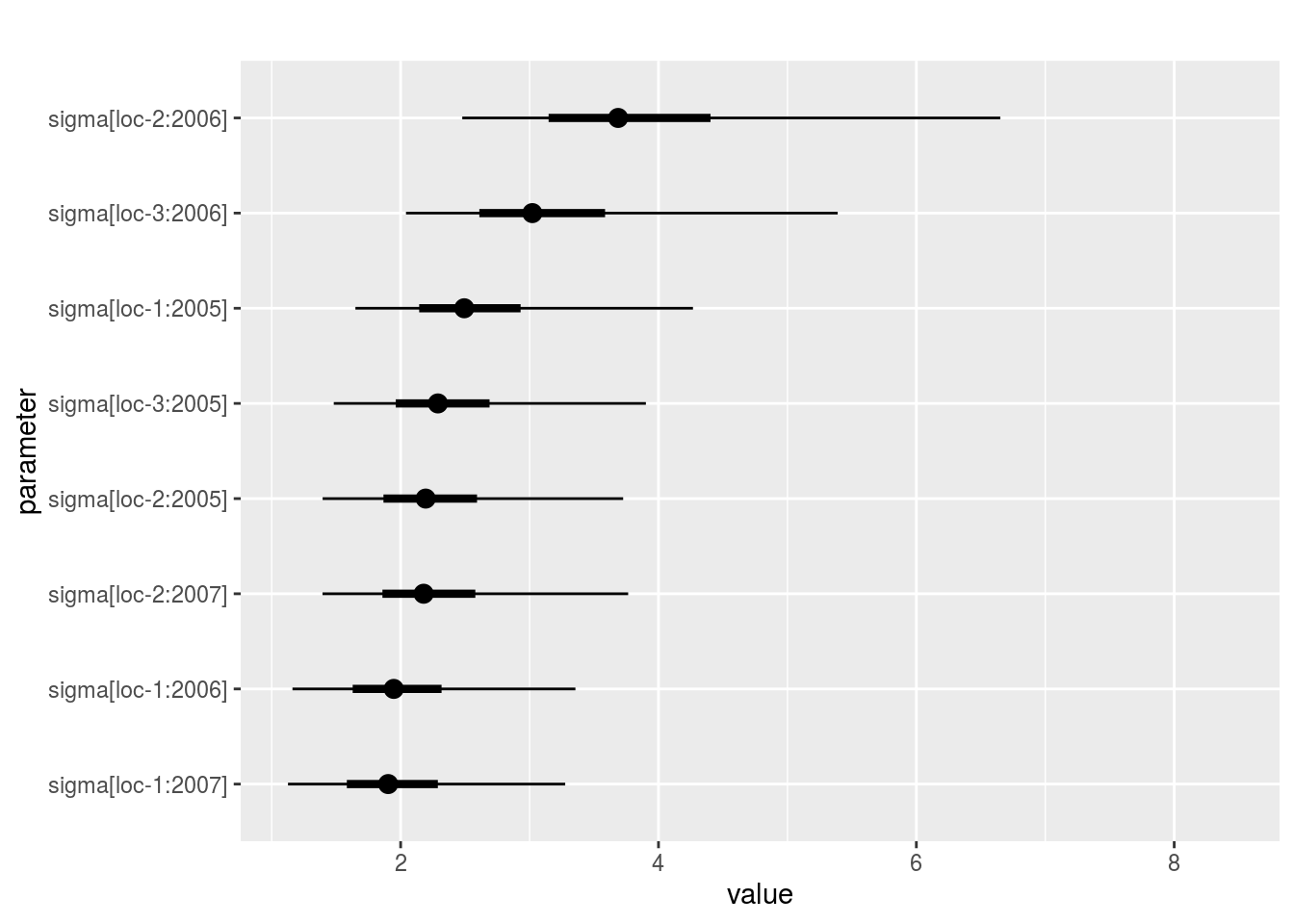

epsilon_ijk : standardised residuals distribution. If the model went well it should be between -2 and 2.

p_out_check_model_bh_intra_location$epsilon_ijk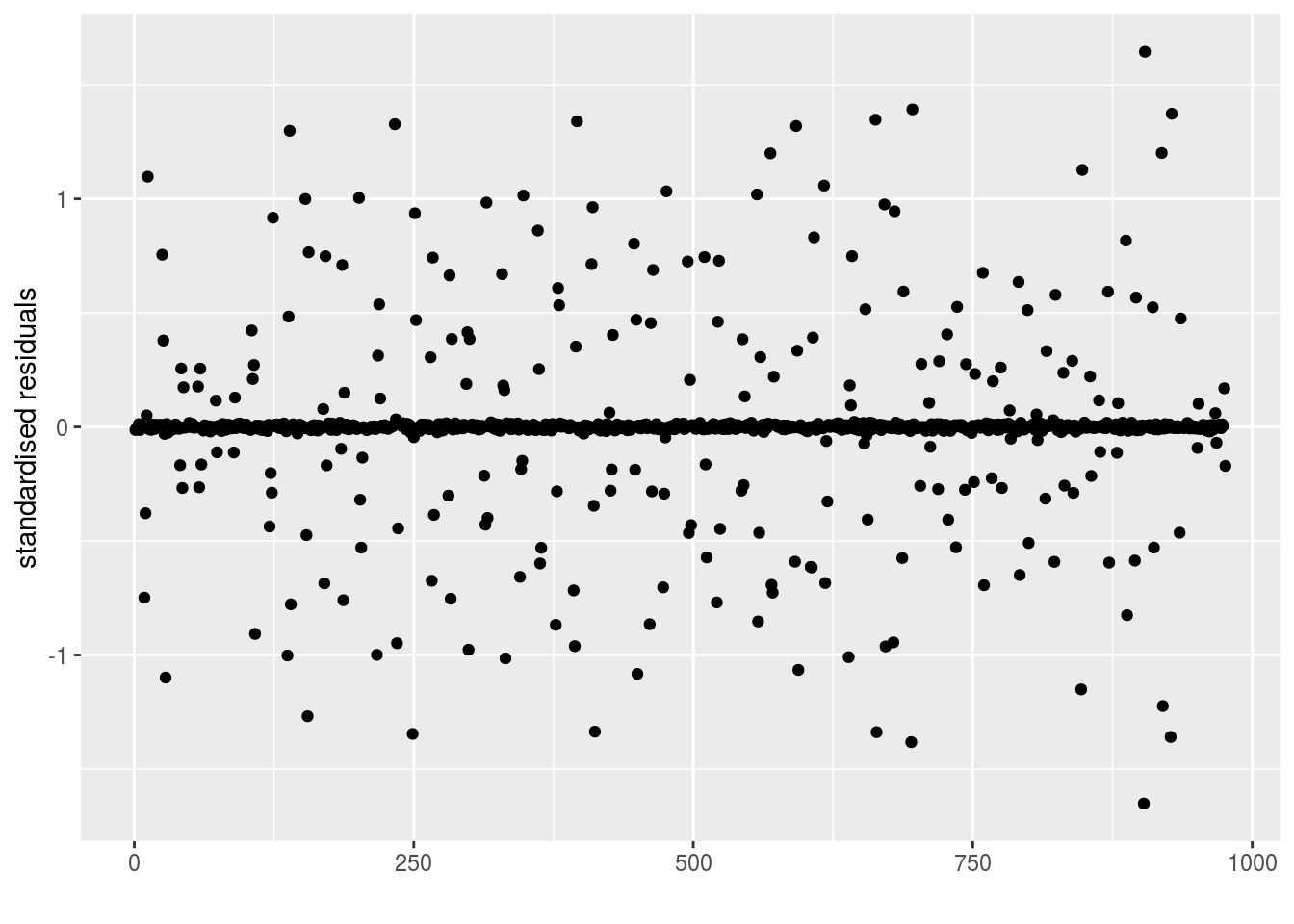

mcmc_not_converge_traceplot_density : a list with the plots of trace and density to check the convergence of the two MCMC only for chains that are not converging detected by the Gelman-Rubin test. If all the chains converge, it is NULL

p_out_check_model_bh_intra_location$mcmc_not_converge_traceplot_density

## NULL

Here all the parameters converged.

When considering p_out_check_model_bh_intra_location_bis, there is no convergence because the MCMC are too small.

p_out_check_model_bh_intra_location_bis = plot(out_check_model_bh_intra_location_bis)

## Distribution of sigma_j in the inverse Gamme distribution are done.

## The mu_ij posterior distributions are done.

## The beta_jk posterior distributions are done.

## The sigma_j posterior distributions are done.

## Trace and density plot for MCMC that did not converged are done.

p_out_check_model_bh_intra_location_bis$mcmc_not_converge_traceplot_density$`sigma\\[loc-15:2006`

## $traceplot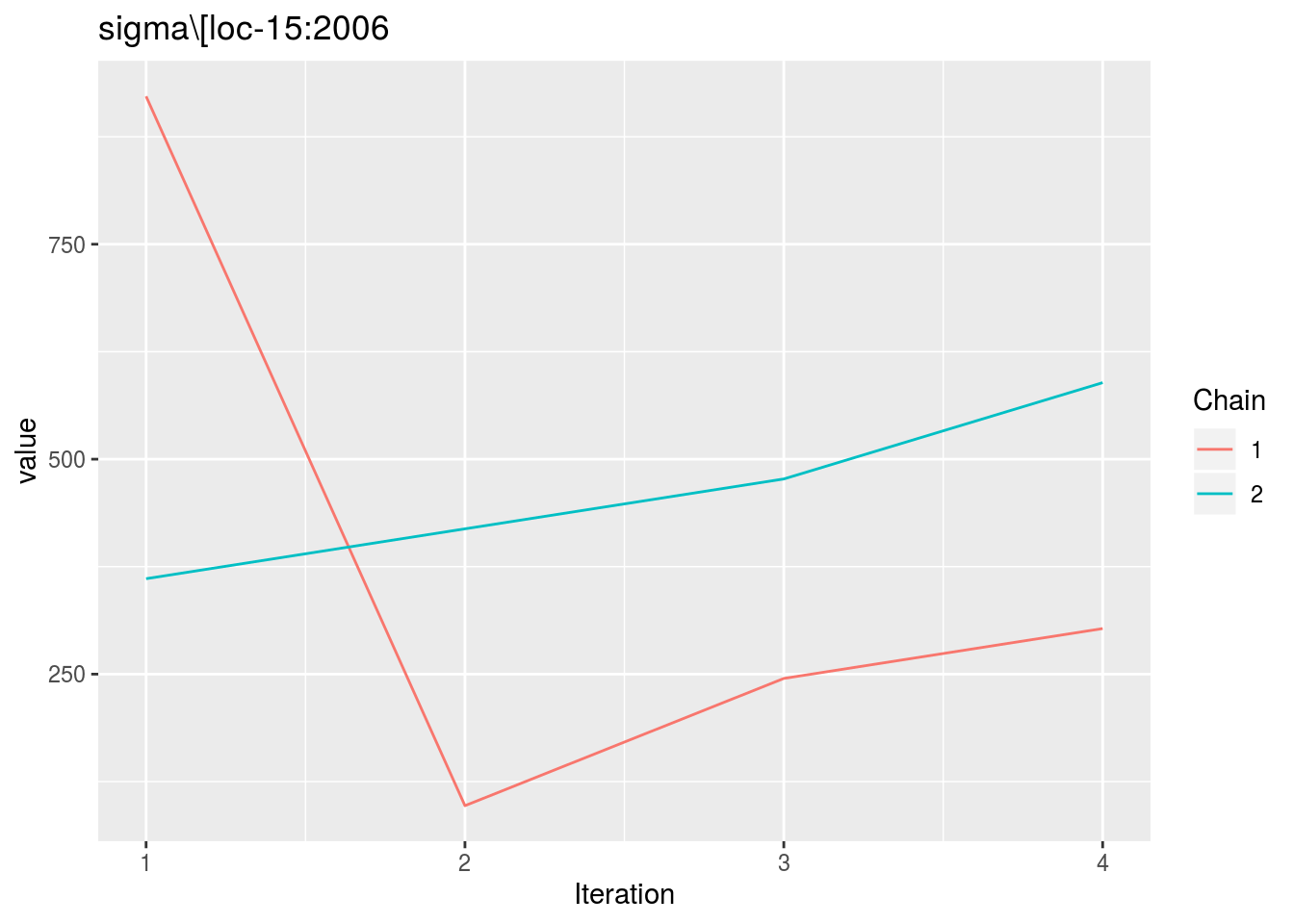

## 
## $density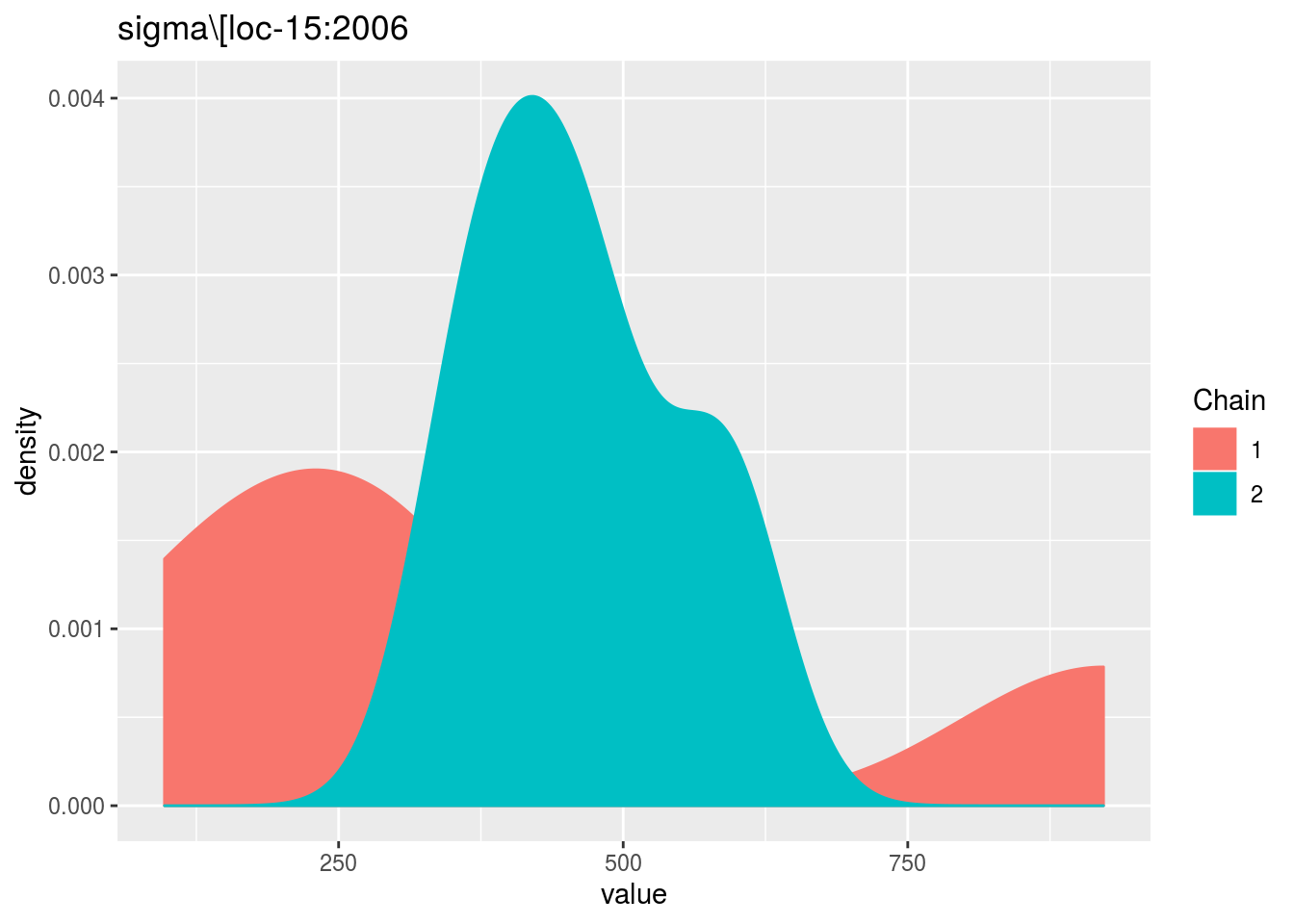

Just for fun, you can compare the posterior medians and the arithmetic means for the mu_ij.

MCMC = out_check_model_bh_intra_location$MCMC
effects = apply(MCMC, 2, median)
mu_ij_estimated = effects[grep("mu",names(effects))]
names(mu_ij_estimated) = sapply(names(mu_ij_estimated), 
                                function(x){  sub("\\]", "", sub("mu\\[", "", x)) } 
                                )

d = dplyr::filter(data_model_bh_intra_location, location != "loc-24")
d = dplyr::filter(d, location != "loc-25")
d = droplevels(d)
environment = paste(as.character(d$location), as.character(d$year), sep = ":")
d$entry = as.factor(paste(as.character(d$germplasm), environment, sep = ","))
mu_ij = tapply(d$mu_ij, d$entry, mean, na.rm = TRUE)

check_data = cbind.data.frame(mu_ij, mu_ij_estimated[names(mu_ij)])

Let’s have a look on the relation between the posterior medians and the arithmetic means. It goes pretty well!

p = ggplot(check_data, aes(x = mu_ij, y = mu_ij_estimated))
p + stat_smooth(method = "lm") + geom_point()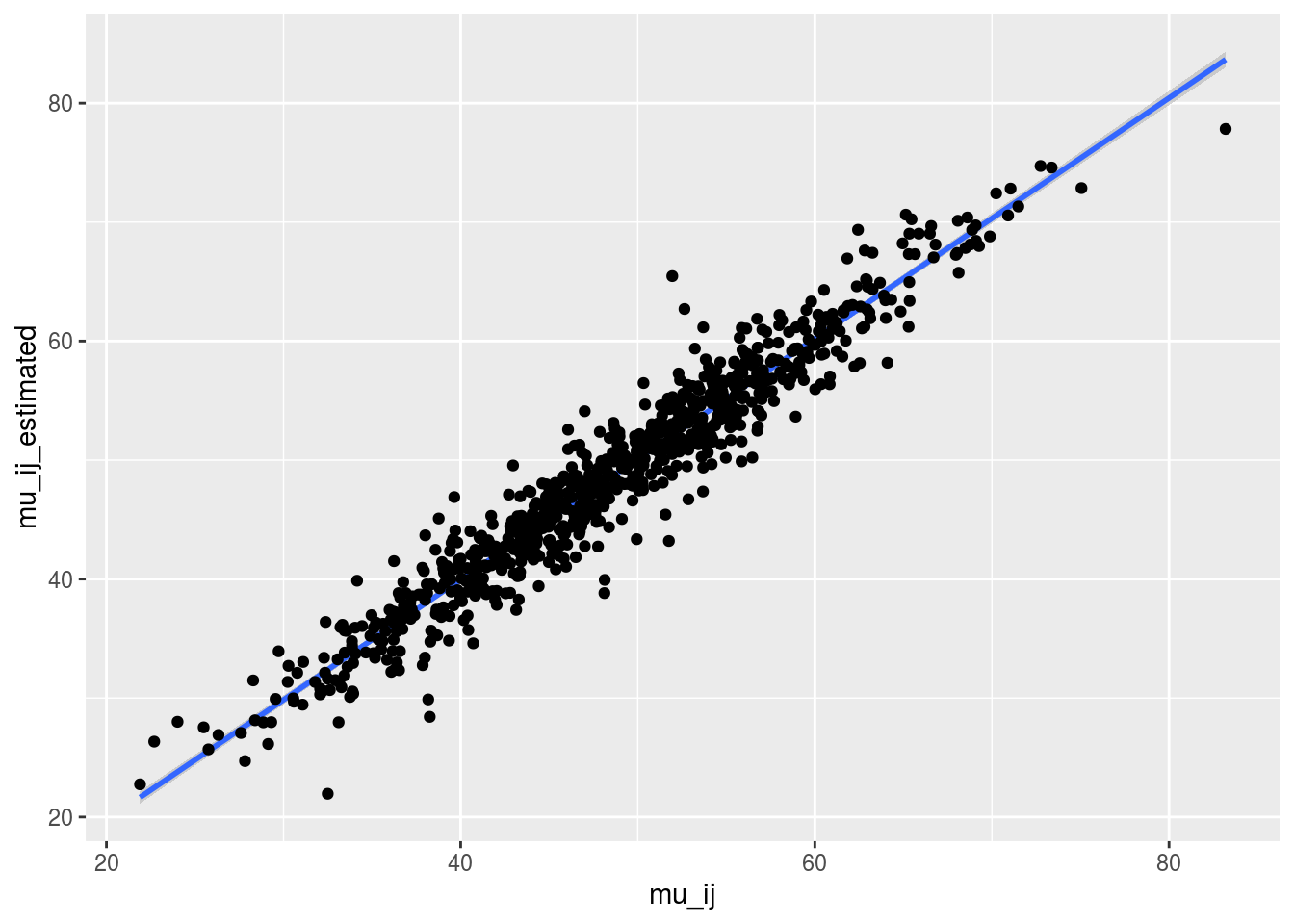

3.5.6.6 Get and visualize mean comparisons

The method to compute mean comparison are explained in section ??.

3.5.6.6.1 Get mean comparisons

Get mean comparisons with mean_comparisons. The theory behind mean comparisons has been explained in section ??.

Below is an example for \(\mu\), the same can be done for \(\beta\).

# out_mean_comparisons_model_bh_intra_location_mu = mean_comparisons(out_check_model_bh_intra_location, parameter = "mu")

# Get at least X groups for loc-11:2007. It may take some time ...
# Get at least X groups for loc-11:2007 is done.
# Get at least X groups for loc-17:2005. It may take some time ...
# Get at least X groups for loc-17:2005 is done.
# Get at least X groups for loc-21:2006. It may take some time ...
# Get at least X groups for loc-21:2006 is done.
# Get at least X groups for loc-9:2006. It may take some time ...
# Get at least X groups for loc-9:2006 is done.

load("./data_PPBstats/out_mean_comparisons_model_bh_intra_location_mu.RData") # To save time

out_mean_comparisons_model_bh_intra_location_mu is a list of three elements:

data_mean_comparisons a list with as many elements as environment.

head(names(out_mean_comparisons_model_bh_intra_location_mu$data_mean_comparisons))

## [1] "loc-1:2005" "loc-1:2006" "loc-1:2007" "loc-2:2005" "loc-2:2006"
## [6] "loc-2:2007"

Each element of the list is composed of two elements:

- `mean.comparisons`

```r
head(out_mean_comparisons_model_bh_intra_location_mu$data_mean_comparisons$`loc-1:2005`$mean.comparisons)
```

```
##                parameter   median groups nb_group alpha alpha.correction
## 1  mu[germ-3,loc-1:2005] 38.42457      a       10  0.05        soft.bonf
## 2  mu[germ-1,loc-1:2005] 41.73724     ab       10  0.05        soft.bonf
## 3 mu[germ-10,loc-1:2005] 45.91424    abc       10  0.05        soft.bonf
## 4 mu[germ-18,loc-1:2005] 47.76006   abcd       10  0.05        soft.bonf
## 5  mu[germ-2,loc-1:2005] 48.10288  abcde       10  0.05        soft.bonf
## 6 mu[germ-19,loc-1:2005] 49.20361 abcdef       10  0.05        soft.bonf
##     entry environment location year
## 1  germ-3  loc-1:2005    loc-1 2005
## 2  germ-1  loc-1:2005    loc-1 2005
## 3 germ-10  loc-1:2005    loc-1 2005
## 4 germ-18  loc-1:2005    loc-1 2005
## 5  germ-2  loc-1:2005    loc-1 2005
## 6 germ-19  loc-1:2005    loc-1 2005
```

- `Mpvalue` : a square matrix with pvalue computed for each pair of parameter.

```r
out_mean_comparisons_model_bh_intra_location_mu$data_mean_comparisons$`loc-1:2005`$Mpvalue[1:3, 1:3]
```

```
##                        mu[germ-3,loc-1:2005] mu[germ-1,loc-1:2005]
## mu[germ-3,loc-1:2005]                      0               0.17505
## mu[germ-1,loc-1:2005]                      0               0.00000
## mu[germ-10,loc-1:2005]                     0               0.00000
##                        mu[germ-10,loc-1:2005]
## mu[germ-3,loc-1:2005]                 0.03940
## mu[germ-1,loc-1:2005]                 0.15185
## mu[germ-10,loc-1:2005]                0.00000
```

data_env_with_no_controls a list with as many elements as environment.

names(out_mean_comparisons_model_bh_intra_location_mu$data_env_with_no_controls)

## [1] "loc-25:2005"

Each list contains mean.comparisons. Note there are no groups displayed. Inded, there were no controls on the environment so no model was run.

head(out_mean_comparisons_model_bh_intra_location_mu$data_env_with_no_controls$`loc-25:2005`$mean.comparisons)

##                 entry germplasm environment block X Y   median
## 1 germ-12,loc-25:2005   germ-12 loc-25:2005     1 4 d 38.02544
## 2 germ-18,loc-25:2005   germ-18 loc-25:2005     1 5 e 44.49495
## 3 germ-19,loc-25:2005   germ-19 loc-25:2005     1 6 f 44.46948
## 4  germ-1,loc-25:2005    germ-1 loc-25:2005     1 3 c 42.32750
## 5 germ-20,loc-25:2005   germ-20 loc-25:2005     1 7 g 35.77590
## 6 germ-21,loc-25:2005   germ-21 loc-25:2005     1 8 h 36.59313
##                 parameter location year
## 1 mu[germ-12,loc-25:2005]   loc-25 2005
## 2 mu[germ-18,loc-25:2005]   loc-25 2005
## 3 mu[germ-19,loc-25:2005]   loc-25 2005
## 4  mu[germ-1,loc-25:2005]   loc-25 2005
## 5 mu[germ-20,loc-25:2005]   loc-25 2005
## 6 mu[germ-21,loc-25:2005]   loc-25 2005

data_env_whose_param_did_not_converge a list with as many elements as environment.

names(out_mean_comparisons_model_bh_intra_location_mu$data_env_whose_param_did_not_converge)

## NULL

Here it is NULL as all parameters converge. Otherwise in each list it is mean.comparisons. Note there are no groups displayed. Inded, the model did not well so no mean comparisons were done.

head(out_mean_comparisons_model_bh_intra_location_mu$data_env_with_no_controls$`loc-5:2005`$mean.comparisons)

## NULL

3.5.6.6.2 Visualize mean comparisons

To see the output, use plot. On each plot, the alpha (type one error) value and the alpha correction are displayed. alpha = Imp means that no differences could be detected. For plot_type = "interaction" and plot_type = "score", it is displayed under the form: alpha | alpha correction.

The ggplot are done for each element of the list coming from mean_comparisons. For each plot_type, it is a list of three lists each with as many elements as environments. For each element of the list, there are as many graphs as needed with nb_parameters_per_plot parameters per graph.

3.5.6.6.2.1 barplot

p_barplot_mu = plot(out_mean_comparisons_model_bh_intra_location_mu, plot_type = "barplot")
names(p_barplot_mu)

## [1] "data_mean_comparisons"                
## [2] "data_env_with_no_controls"            
## [3] "data_env_whose_param_did_not_converge"

From data_mean_comparisons, only environments where all MCMC converged are represented.

Letters are displayed on each bar. Parameters that do not share the same letters are different based on type I error (alpha) and alpha correction.

The error I (alpha) and the alpha correction are displayed in the title. alpha = Imp means that no significant differences coumd be detected.

p = p_barplot_mu$data_mean_comparisons

head(names(p))

## [1] "loc-1:2005" "loc-1:2006" "loc-1:2007" "loc-2:2005" "loc-2:2006"
## [6] "loc-2:2007"

p_env = p$`loc-1:2005`
names(p_env)

## [1] "1" "2" "3" "4"

p_env$`1`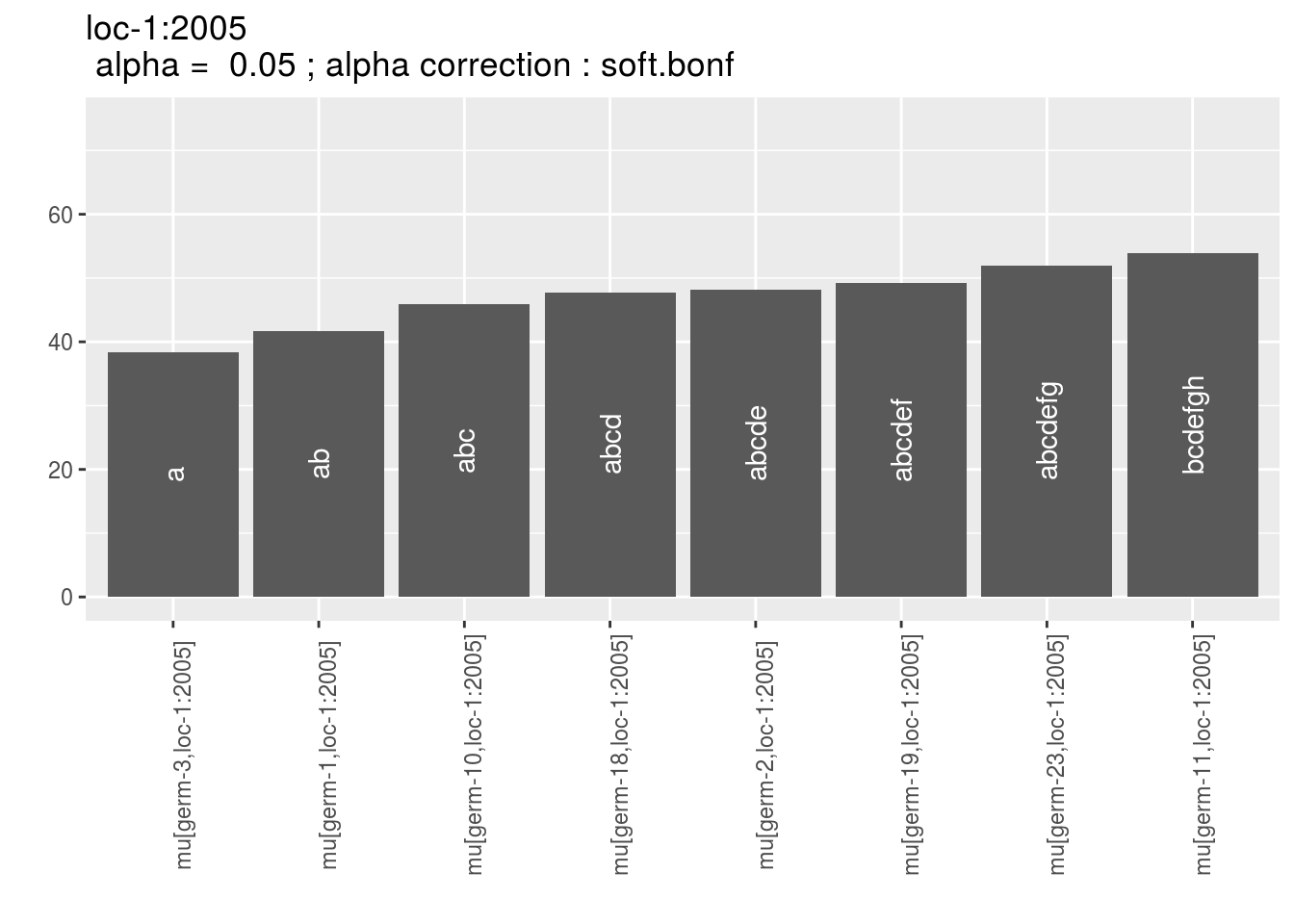

p_env$`2`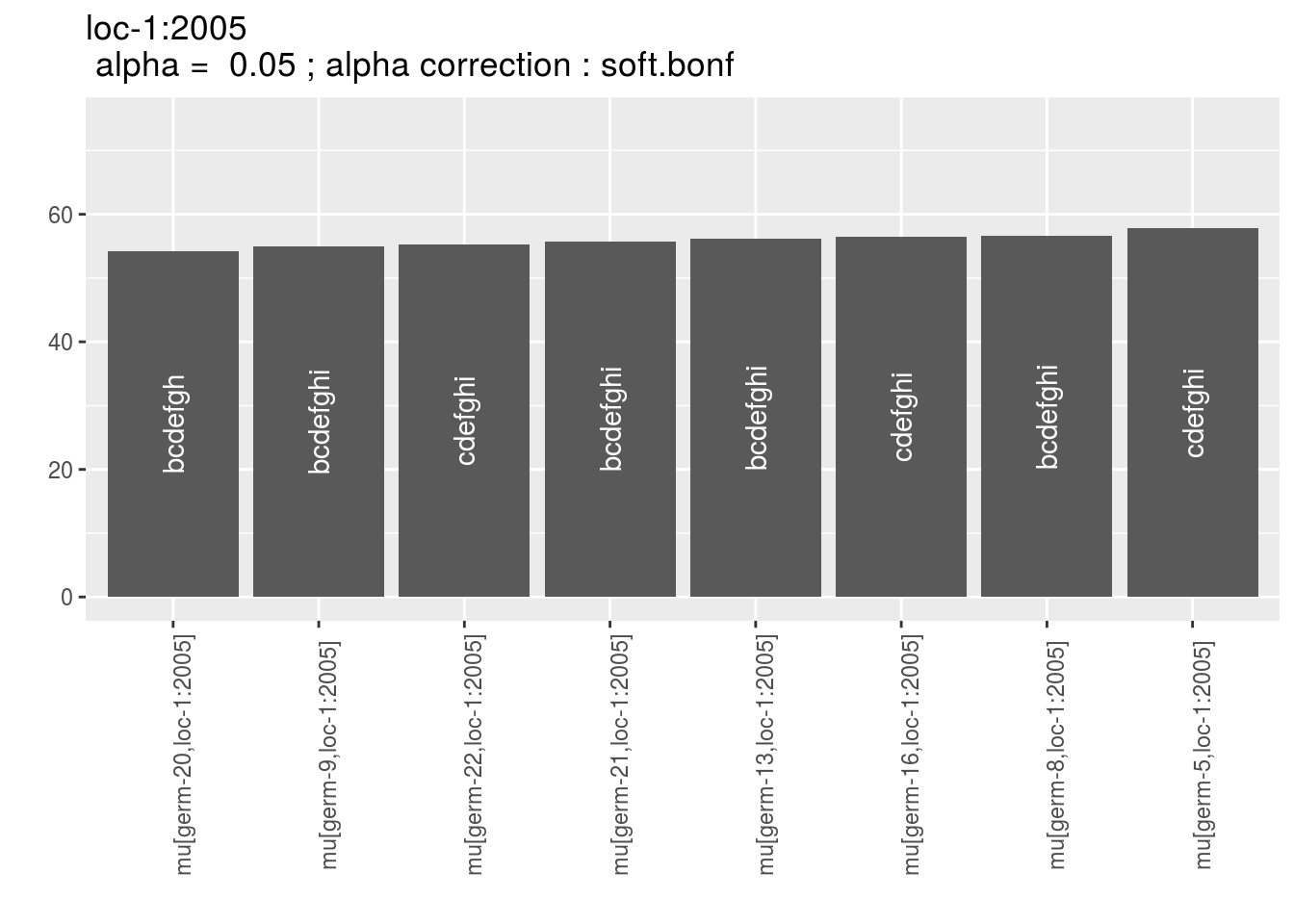

p_env$`3`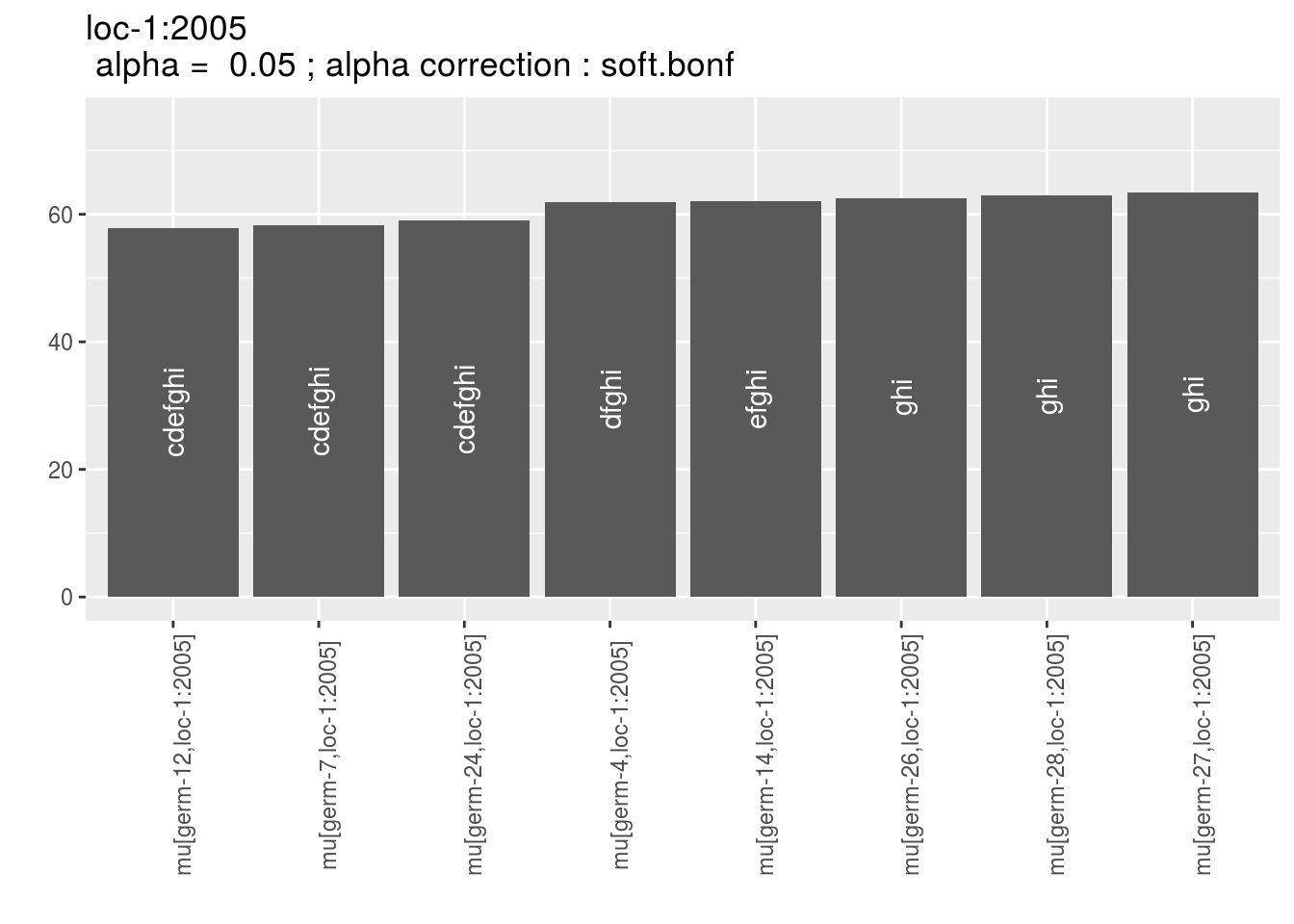

p_env$`4`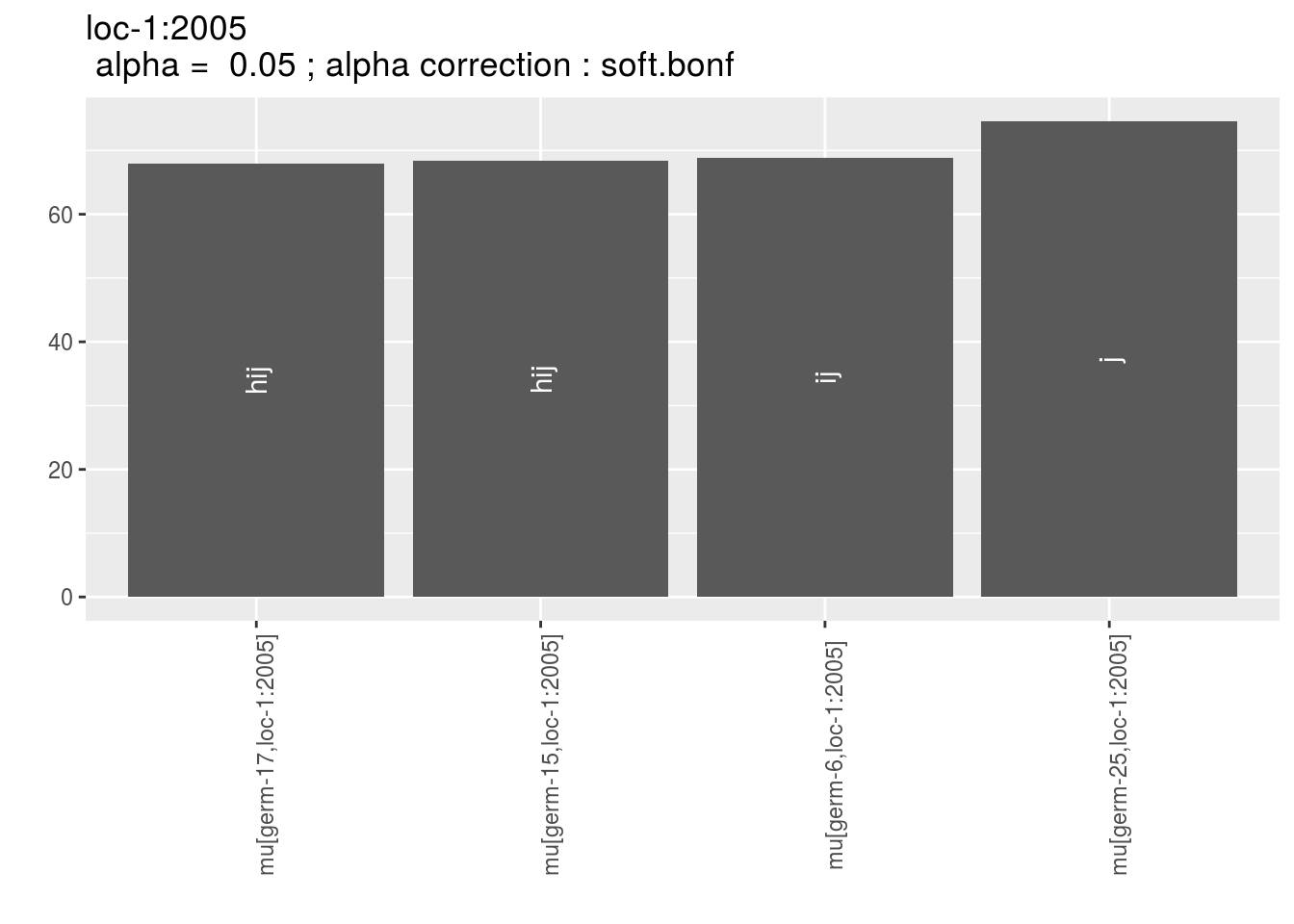

For data_env_with_no_controls, only environments where there were no controls are represented.

p_barplot_mu$data_env_with_no_controls

## $`loc-25:2005`
## $`loc-25:2005`$`1`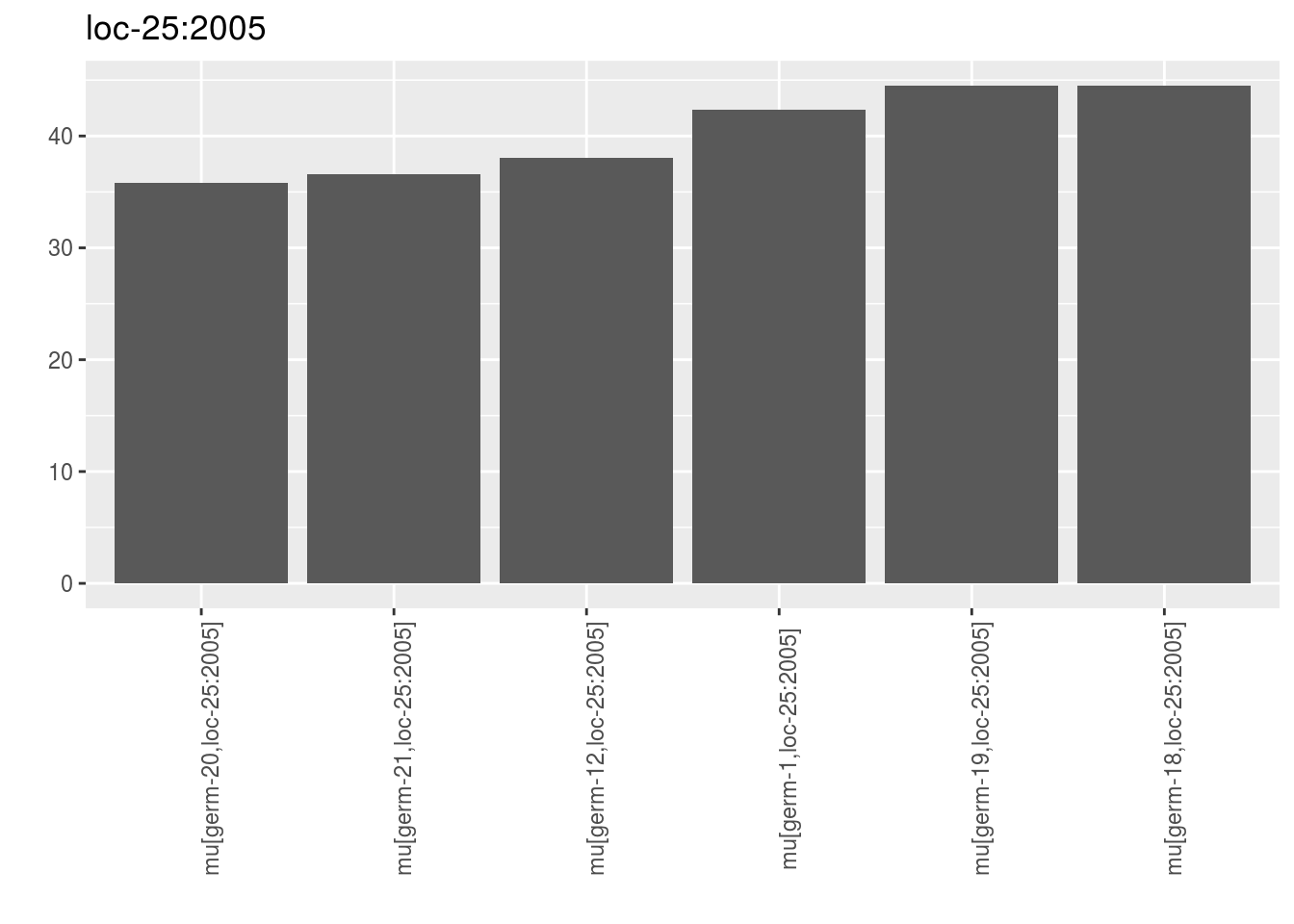

For data_env_whose_param_did_not_converge, only environments where MCMC did not converge are represented.

p_barplot_mu$data_env_whose_param_did_not_converge

## list()

3.5.6.6.2.2 interaction

With plot_type = "interaction", you can display the year effect as well as detect groups. One group is represented by one vertical line. Germplasms which share the same group are not different. Germplasms which do not share the same groupe are different (Section ??).

The ggplot are done for each element of the list coming rom mean_comparisons.

For each plot_type, it is a list of three elements being lists with as many elements as environment.

For each element of the list, there are as many graph as needed with nb_parameters_per_plot parameters per graph.

p_interaction = plot(out_mean_comparisons_model_bh_intra_location_mu, plot_type = "interaction")

head(names(p_interaction$data_mean_comparisons))

## [1] "loc-1"  "loc-10" "loc-11" "loc-12" "loc-13" "loc-14"

p_env = p_interaction$data_mean_comparisons$`loc-1`
names(p_env)

## [1] "1" "2" "3" "4"

p_env$`1`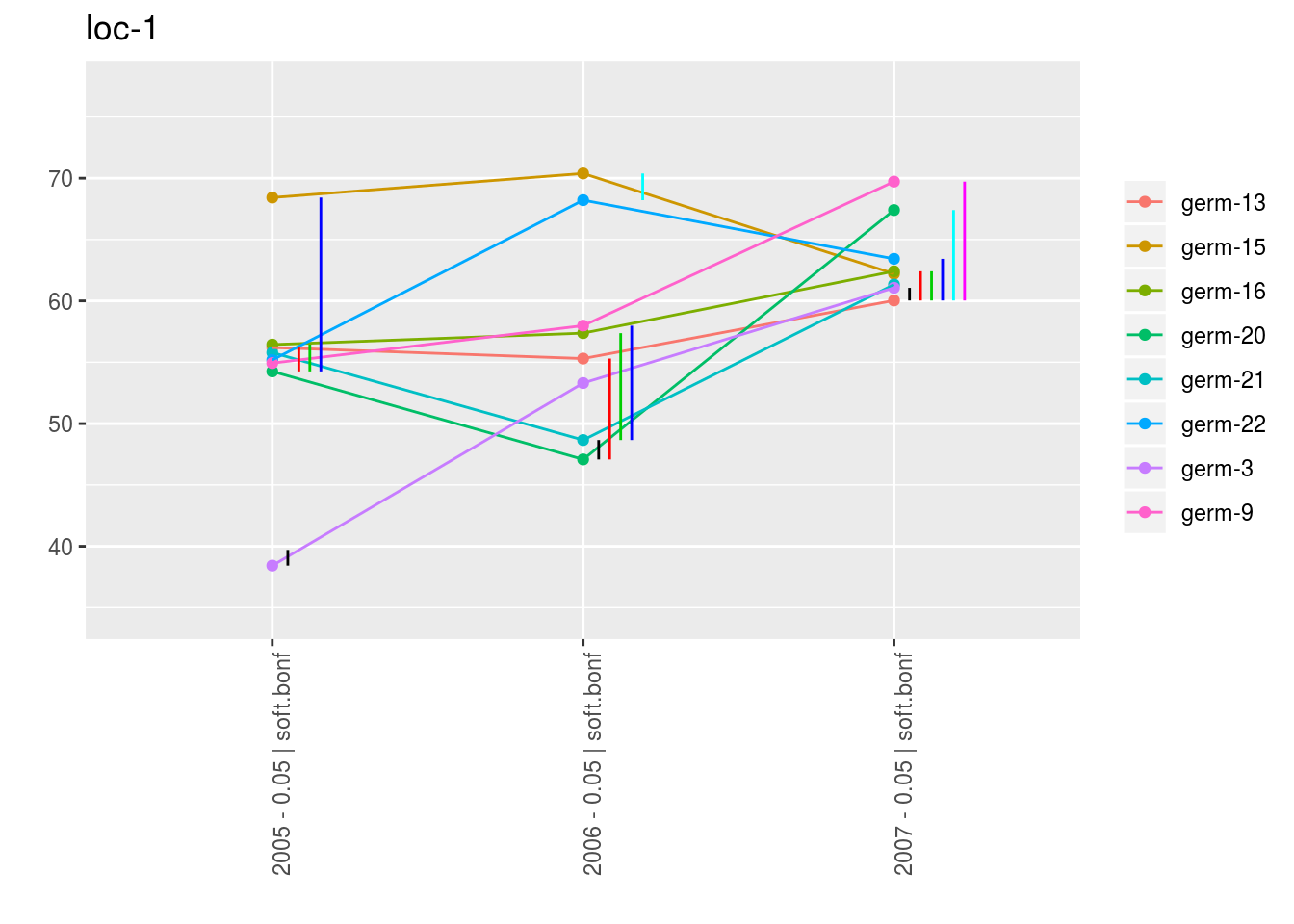

p_env$`2`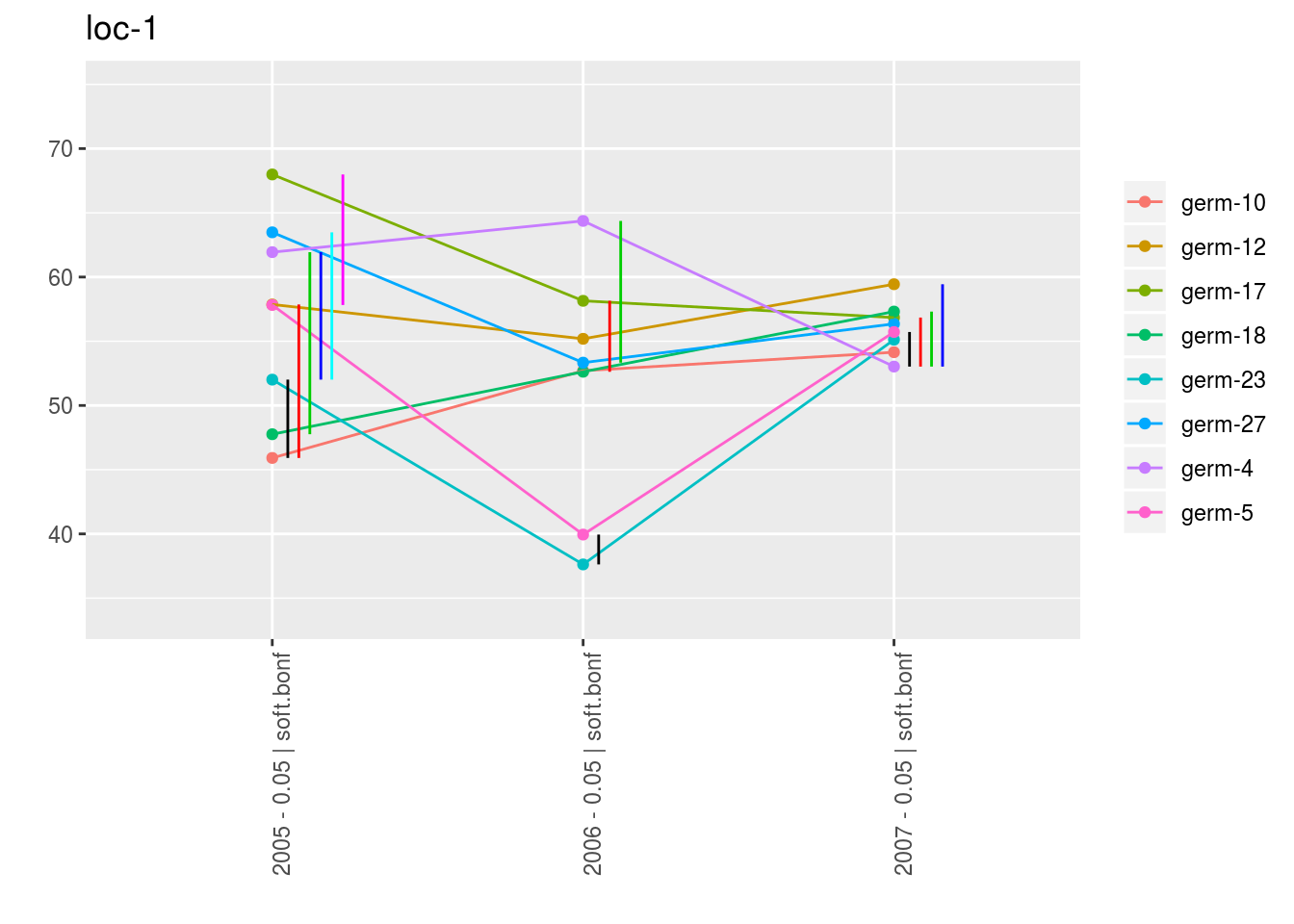

p_env$`3`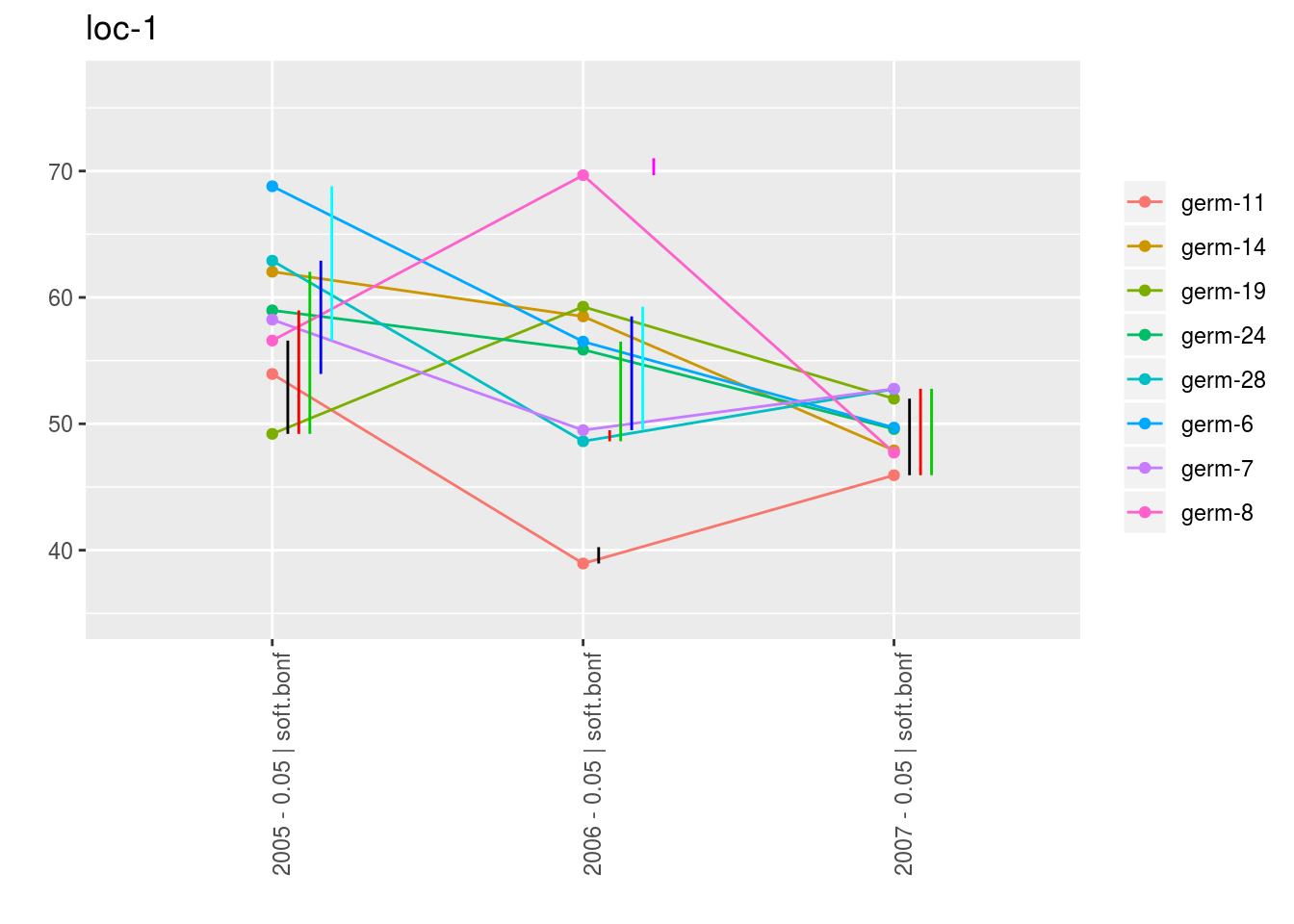

p_env$`4`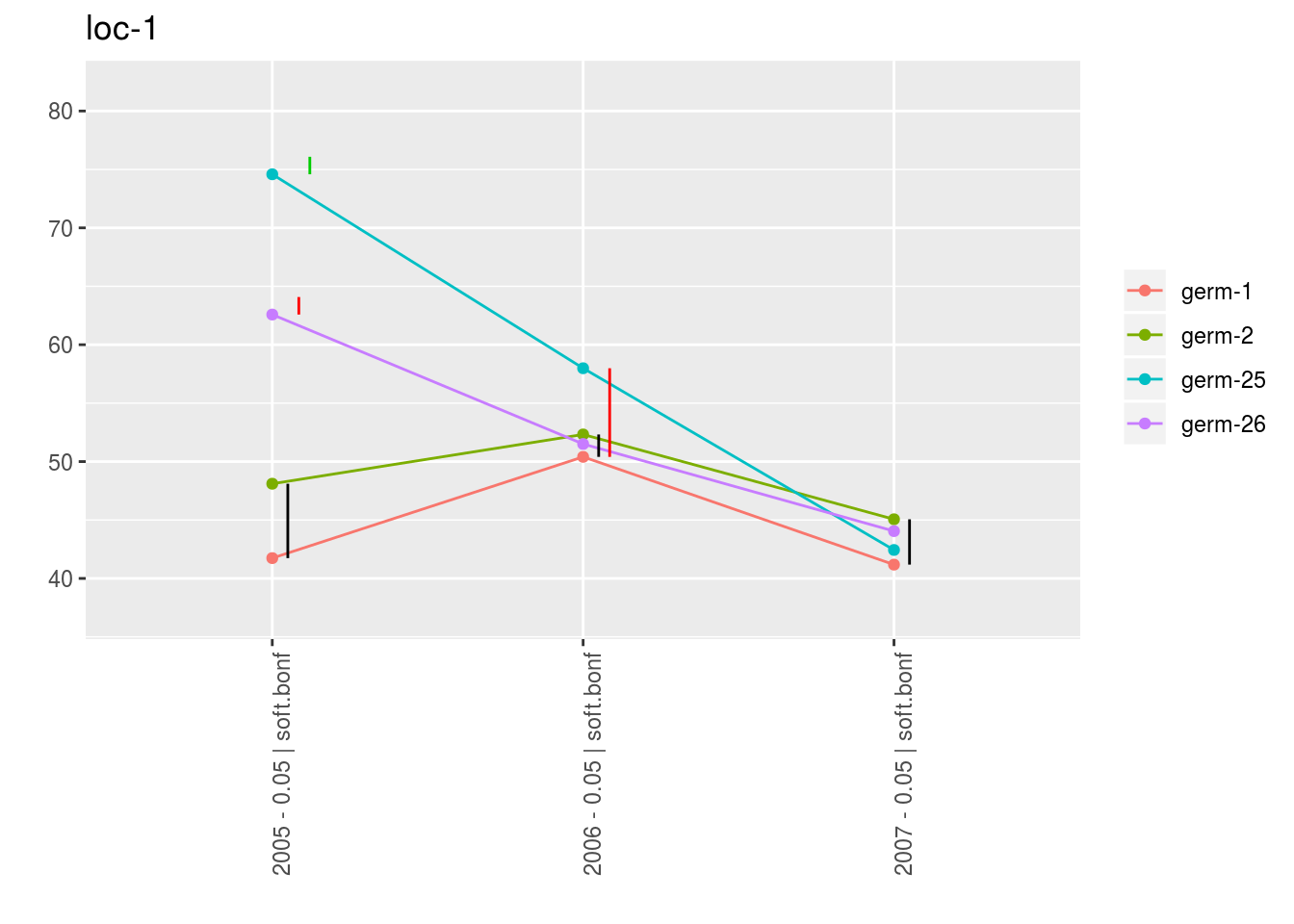

3.5.6.6.3 score

For the score, more entries are displayed. An high score means that the entry was in a group with an high mean. A low socre means that the entry was in a group with an low mean. In the legend, the score goes from 1 (first group) to the number of groups of significativity. This plot is useful to look at year effects.

p_score = plot(out_mean_comparisons_model_bh_intra_location_mu, plot_type = "score")

head(names(p_score))

## [1] "loc-1"  "loc-10" "loc-11" "loc-12" "loc-13" "loc-14"

p_env = p_score$`loc-1`
names(p_env)

## [1] "1" "2" "3" "4"

p_env$`1`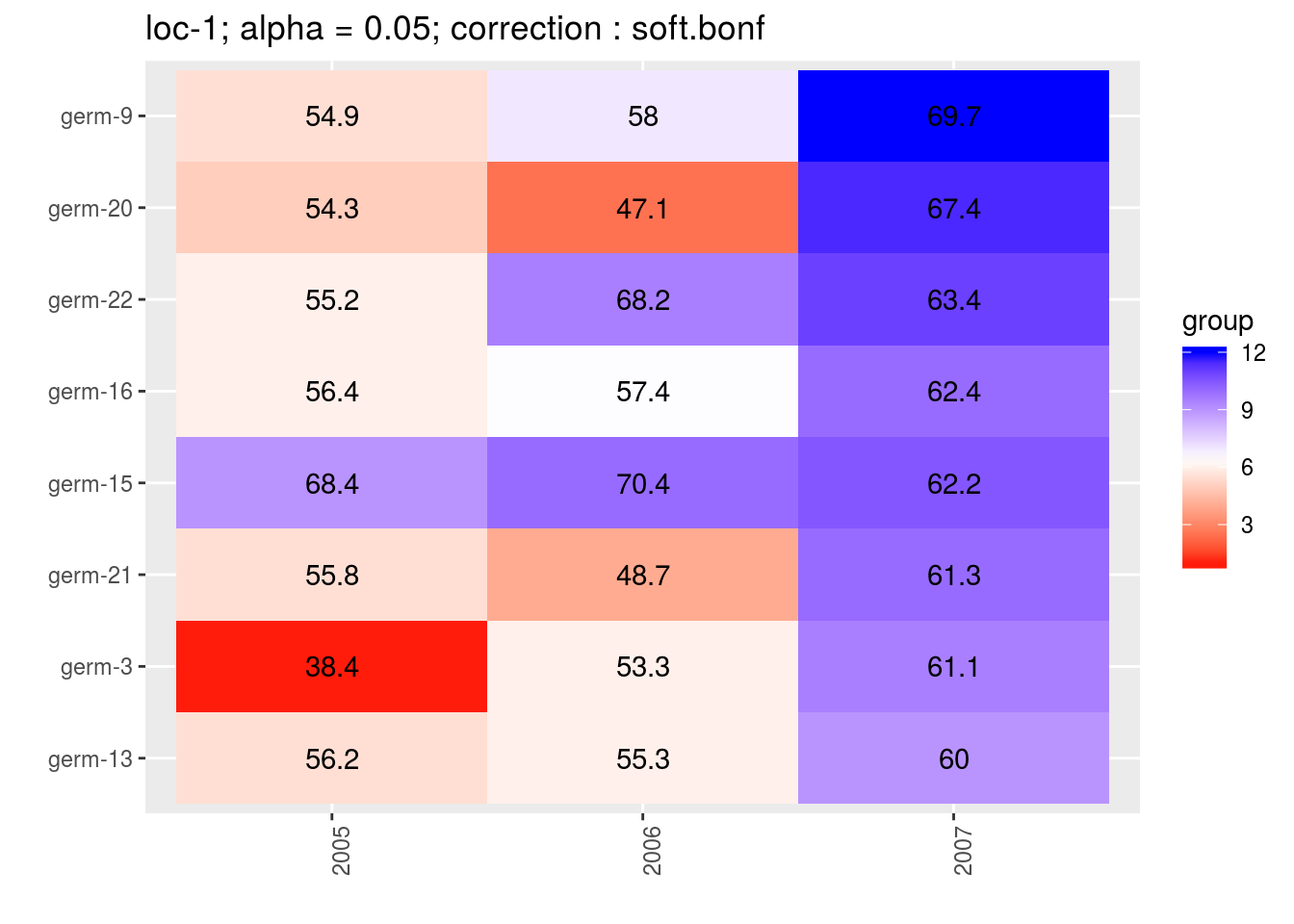

p_env$`2`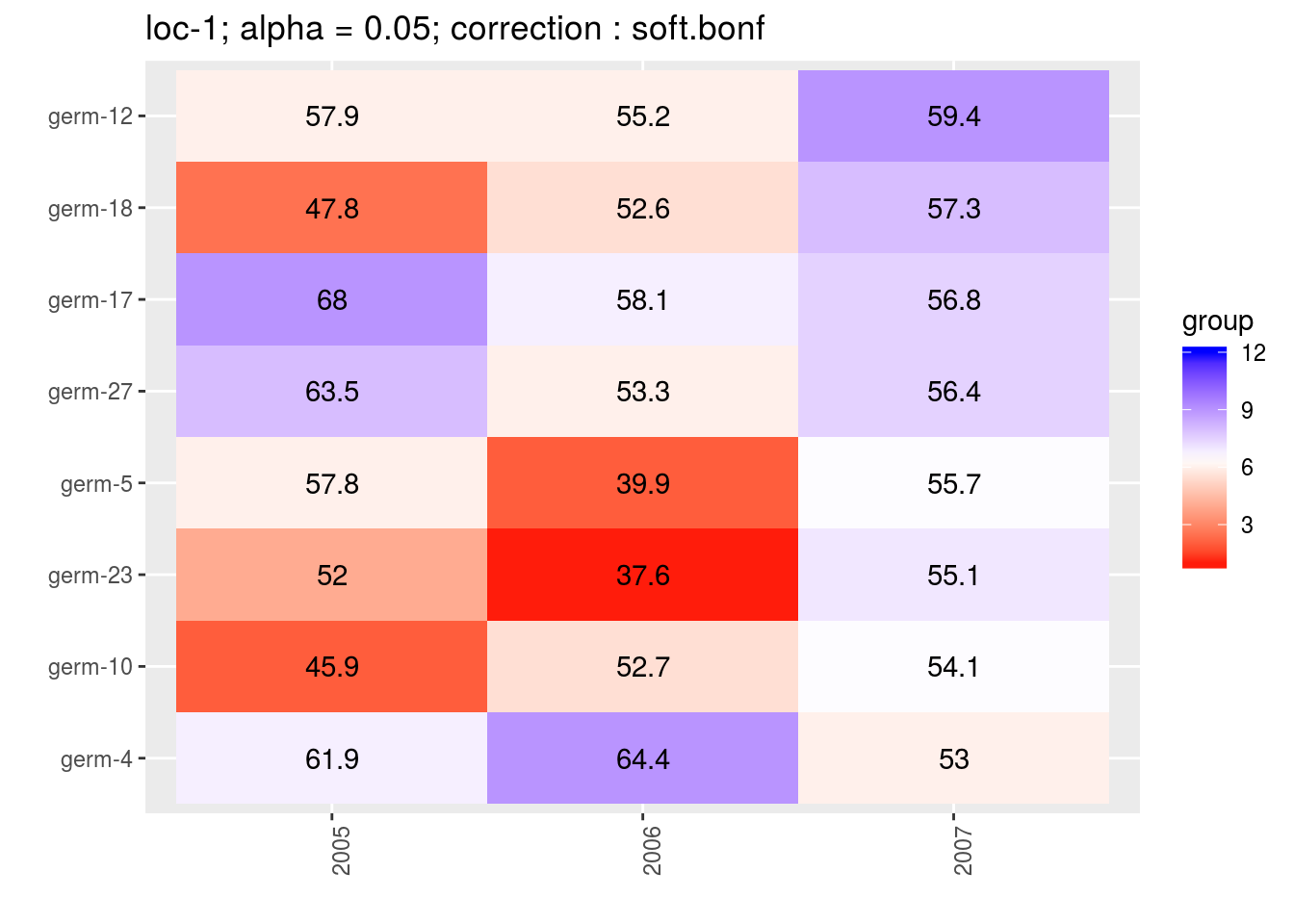

p_env$`3`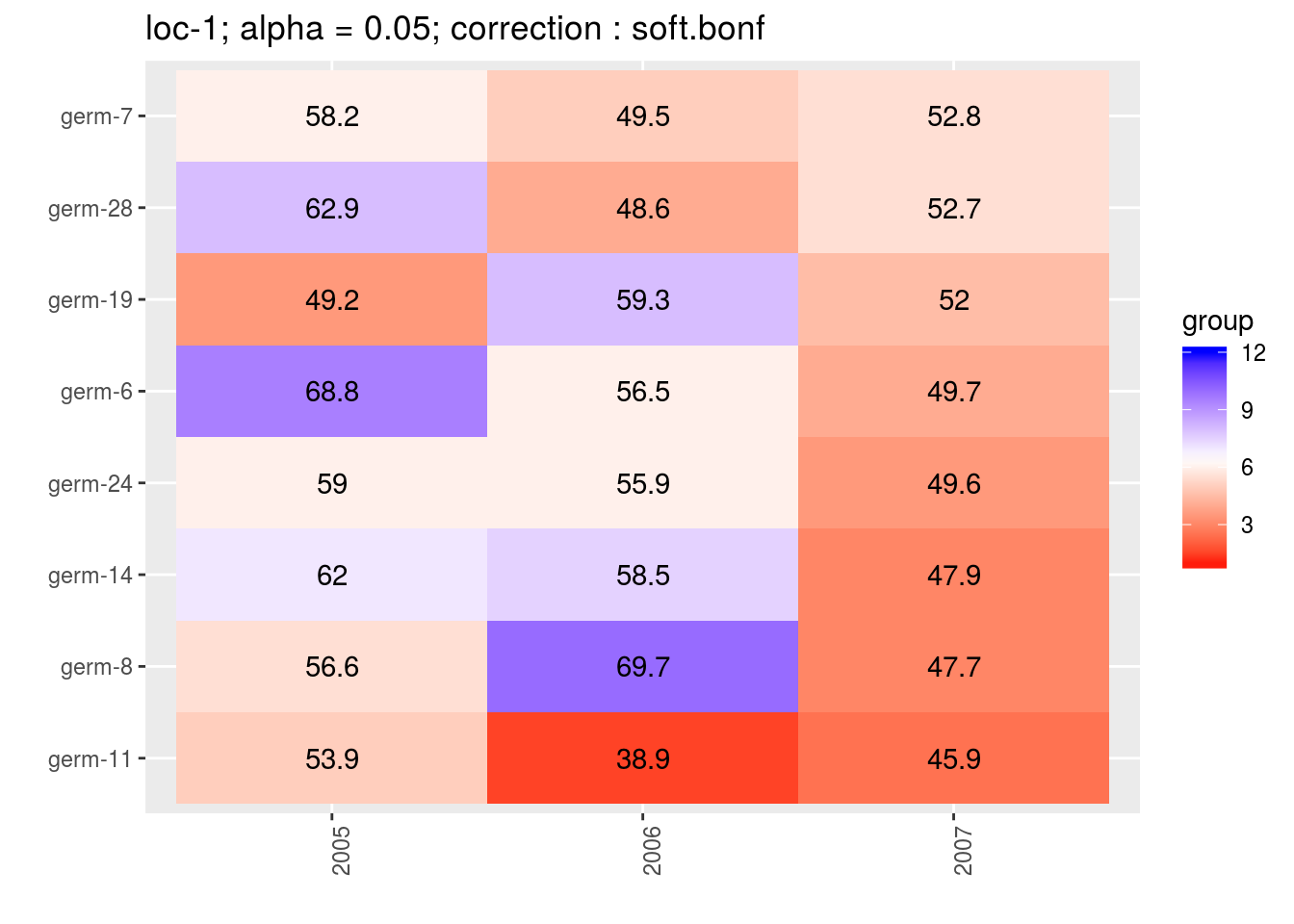

p_env$`4`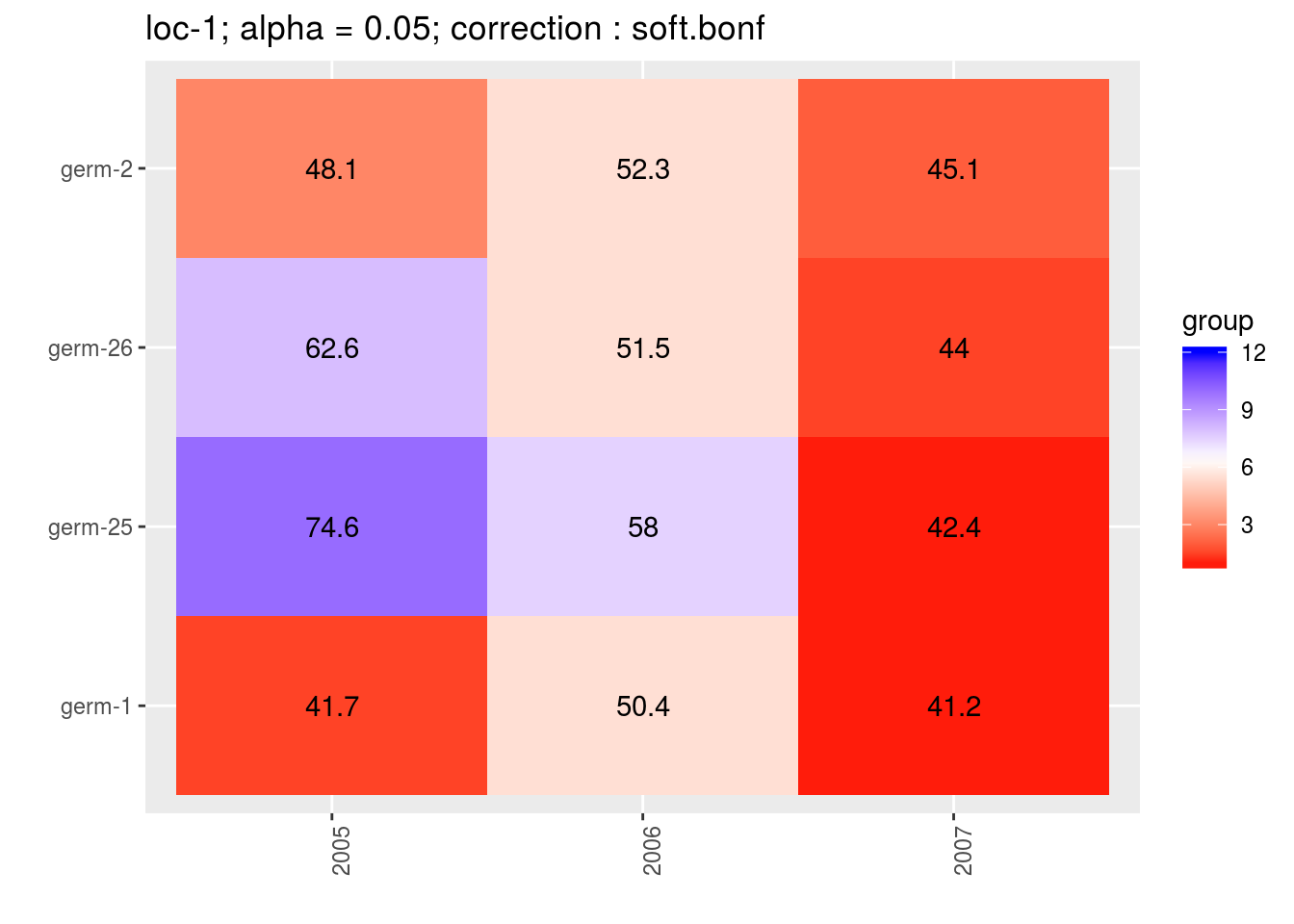

3.5.6.7 Apply the workflow to several variables

If you wish to apply the model_bh_intra_location workflow to several variables, you can use lapply with the following code :

workflow_model_bh_intra_location = function(x){
  out_model_bh_intra_location = model_bh_intra_location(data = data_model_bh_intra_location, variable = x, return.epsilon = TRUE)
  
  out_check_model_bh_intra_location = check_model(out_model_bh_intra_location)
  p_out_check_model_bh_intra_location = plot(out_check_model_bh_intra_location)
  
  out_mean_comparisons_model_bh_intra_location_mu = mean_comparisons(out_check_model_bh_intra_location, parameter = "mu")
  p_barplot_mu = plot(out_mean_comparisons_model_bh_intra_location_mu, plot_type = "barplot")
  p_interaction = plot(out_mean_comparisons_model_bh_intra_location_mu, plot_type = "interaction")
  p_score = plot(out_mean_comparisons_model_bh_intra_location_mu, plot_type = "score")
  
  out = list(
    "out_model_bh_intra_location" = out_model_bh_intra_location,
    "out_check_model_bh_intra_location" = out_check_model_bh_intra_location,
    "p_out_check_model_bh_intra_location" = p_out_check_model_bh_intra_location,
    "out_mean_comparisons_model_bh_intra_location_mu" = out_mean_comparisons_model_bh_intra_location_mu,
    "p_barplot_mu" = p_barplot_mu,
    "p_interaction" = p_interaction,
    "p_score" = p_score
    )
  return(out)
}

## Not run because of memory and time issues !
# vec_variables = c("y1", "y2", "y3")
#
# out = lapply(vec_variables, workflow_model_bh_intra_location)
# names(out) = vec_variables

References

Desclaux, D., J. M. Nolot, Y. Chiffoleau, C. Leclerc, and E. Gozé. 2008. “Changes in the Concept of Genotype X Environment Interactions to Fit Agriculture Diversification and Decentralized Participatory Plant Breeding: Pluridisciplinary Point of View.” Euphytica 163: 533–46.

Plummer, M. 2008. “Penalized Loss Functions for Bayesian Model Comparison.” Biostatistics 9 (3): 523–39.

Rivière, P., J.C. Dawson, I. Goldringer, and O. David. 2015. “Hierarchical Bayesian Modeling for Flexible Experiments in Decentralized Participatory Plant Breeding.” Crop Science 55 (3).

Rodrı'guez-Álvarez, X.M., M. P. Boer, F. A. van Eeuwijk, and P. H. C. Eilers. 2016. “Spatial Models for Field Trials.” ArXiv E-Prints, July.

Spiegelhalter, D. J., N. G. Best, B. P. Carlin, and A. Van Der Linde. 2002. “Bayesian Measures of Model Complexity and Fit.” Journal of the Royal Statistical Society: Series B (Statistical Methodology) 64 (4): 583–639.

Zystro, Jared, Micaela Colley, and Julie Dawson. 2018. “Alternative Experimental Designs for Plant Breeding.” In, 87–117. https://doi.org/10.1002/9781119521358.ch3.

Note that it is quite different from Rivière et al. (2015) where the model was written only for two blocks. Here there is no restriction on the number of blocks.↩